题目内容
【题目】设函数![]() ,
, ![]() ,其中
,其中![]() R,
R, ![]() …为自然对数的底数.
…为自然对数的底数.
(Ⅰ)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)求证: ![]() (参考数据:
(参考数据: ![]() ).
).
【答案】(1)![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)先构造函数![]() ,再对其求导得到
,再对其求导得到![]() 然后分
然后分![]() 和
和![]() 两种情形分类讨论进行分析求解:
两种情形分类讨论进行分析求解:
(2)借助(1)的结论,当![]() 时,
时, ![]() 对
对![]() 恒成立, 再令
恒成立, 再令![]() ,得到
,得到![]() 即
即![]() ; 又由(Ⅰ)知,当
; 又由(Ⅰ)知,当![]() 时,则
时,则![]() 在
在![]() 递减,在
递减,在![]() 递增,则
递增,则![]() ,即
,即![]() ,又
,又![]() ,即
,即![]() ,令
,令![]() ,即
,即![]() ,则
,则![]() ,
,
故有![]() .
.
解:
(Ⅰ)令![]() ,则
,则![]()
①若![]() ,则
,则![]() ,
, ![]() ,
, ![]() 在
在![]() 递增,
递增, ![]() ,
,
即![]() 在
在 ![]() 恒成立,满足,所以
恒成立,满足,所以![]() ;
;
②若![]() ,
, ![]() 在
在![]() 递增,
递增, ![]() 且
且![]()
且![]() 时,
时, ![]() ,则
,则![]() 使
使![]() ,
,
则![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
所以当![]() 时
时![]() ,即当
,即当![]() 时,
时, ![]() ,
,
不满足题意,舍去;
综合①,②知![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)由(Ⅰ)知,当![]() 时,
时, ![]() 对
对恒成立,
令![]() ,则
,则![]() 即
即![]() ;
;
由(Ⅰ)知,当![]() 时,则
时,则![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
则![]() ,即
,即![]() ,又
,又![]() ,即
,即![]() ,
,
令![]() ,即
,即![]() ,则
,则![]() ,
,
故有![]() .
.

【题目】有人收集了七月份的日平均气温![]() (摄氏度)与某次冷饮店日销售额
(摄氏度)与某次冷饮店日销售额![]() (百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
(百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
日平均气温 | 31 | 32 | 33 | 34 | 35 |
日销售额 | 5 | 6 | 7 | 8 | 10 |
由资料可知,![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,给出下列说法:
,给出下列说法:
①![]() ;
;
②日销售额![]() (百元)与日平均气温
(百元)与日平均气温![]() (摄氏度)成正相关;
(摄氏度)成正相关;
③当日平均气温为![]() 摄氏度时,日销售额一定为
摄氏度时,日销售额一定为![]() 百元.
百元.
其中正确说法的序号是______.
【题目】在改革开放40年成就展上某地区某农产品近几年的产量统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)根据线性回归方程预测2020年该地区该农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为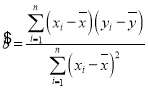 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留到小数点后两位)
,计算结果保留到小数点后两位)