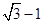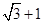题目内容
设直线 的斜率为2且过抛物线
的斜率为2且过抛物线 的焦点F,又与
的焦点F,又与 轴交于点A,
轴交于点A, 为坐标原点,若
为坐标原点,若 的面积为4,则抛物线的方程为:
的面积为4,则抛物线的方程为:
A. | B. | C. | D.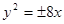 |
D
解析试题分析:解:抛物线y2=ax(a≠0)的焦点F坐标为(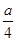 ,0),则直线l的方程为y=2(x-
,0),则直线l的方程为y=2(x-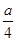 ),它与y轴的交点为A(0,-
),它与y轴的交点为A(0,-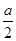 ),所以△OAF的面积为
),所以△OAF的面积为 所以抛物线方程为
所以抛物线方程为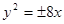 故选D.
故选D.
考点:抛物线的标准方程
点评:本题主要考查了抛物线的标准方程,点斜式求直线方程等.考查学生的数形结合的思想的运用和基础知识的灵活运用.

练习册系列答案
相关题目
已知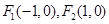 为椭圆
为椭圆 的两个焦点,若椭圆上一点
的两个焦点,若椭圆上一点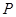 满足
满足 ,则椭圆的离心率
,则椭圆的离心率 ( )
( )
A.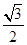 | B.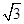 | C. | D. |
已知正三角形AOB的顶点A,B在抛物线 上,O为坐标原点,则
上,O为坐标原点,则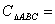 ( )
( )
A.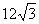 | B. | C. | D. |
若椭圆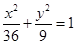 的弦被点
的弦被点 平分,则此弦所在的直线方程是 ( )
平分,则此弦所在的直线方程是 ( )
A.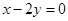 | B.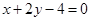 |
C.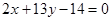 | D. |
双曲线 的渐近线的方程是( )
的渐近线的方程是( )
A. | B. | C. | D. |
已知点 是抛物线
是抛物线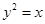 的焦点,
的焦点,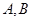 是抛物线上的两点,
是抛物线上的两点,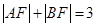 ,则线段
,则线段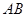 的中点到
的中点到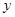 轴的距离为( )
轴的距离为( )
A. | B.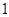 | C.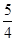 | D.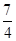 |
 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和 轴交于点A,若△OAF(O为坐标原点)的面积为4, 则抛物线方程为
轴交于点A,若△OAF(O为坐标原点)的面积为4, 则抛物线方程为



 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于
交双曲线右支于 点,若
点,若 为线段
为线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则 与
与 的大小关系为( )
的大小关系为( )



 和
和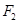 分别是双曲线
分别是双曲线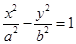 (
( ,
, )的两个焦点,
)的两个焦点, 和
和 是以
是以 为圆心,以
为圆心,以 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( )