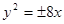题目内容
从双曲线 的左焦点
的左焦点 引圆
引圆 的切线,切点为
的切线,切点为 ,延长
,延长 交双曲线右支于
交双曲线右支于 点,若
点,若 为线段
为线段 的中点,
的中点, 为坐标原点,则
为坐标原点,则 与
与 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D.不确定 |
B
解析试题分析:点P置于第一象限.设F1是双曲线的右焦点,连接PF1.由M、O分别为FP、FF1的中点,知|MO|= |PF1|.由双曲线定义,知|PF|-|PF1|=2a,|FT|=
|PF1|.由双曲线定义,知|PF|-|PF1|=2a,|FT|= =b.由此知|MO|-|MT|=
=b.由此知|MO|-|MT|= (|PF1|-|PF|)+|FT|=b-a
(|PF1|-|PF|)+|FT|=b-a
解:将点P置于第一象限.
设F1是双曲线的右焦点,连接PF1,∵M、O分别为FP、FF1的中点,∴|MO|= |PF1|,又由双曲线定义得, |PF|-|PF1|=2a, |FT|=
|PF1|,又由双曲线定义得, |PF|-|PF1|=2a, |FT|= =b.故|MO|-|MT|=
=b.故|MO|-|MT|= |PF1|-|MF|+|FT|=
|PF1|-|MF|+|FT|= (|PF1|-|PF|)+|FT|=b-a.故选C.
(|PF1|-|PF|)+|FT|=b-a.故选C.
考点:直线与圆锥曲线
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
已知双曲线 的中心为原点,
的中心为原点, 是
是 的焦点,过
的焦点,过 的直线
的直线 与
与 相交于
相交于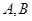 两点,且
两点,且 的中点为
的中点为 ,则
,则 的方程为( )
的方程为( )
A. | B. | C. | D. |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
抛物线 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦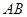 中点
中点 在准线
在准线 上的射影为
上的射影为 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知椭圆 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )
| A.2 | B.3 | C.5 | D.7 |
已知直线与平面 平行,P是直线
平行,P是直线 上的一点,平面
上的一点,平面 内的动点B满足:PB与直线
内的动点B满足:PB与直线 成
成 。那么B点轨迹是
。那么B点轨迹是
| A.双曲线 | B.椭圆 | C.抛物线 | D.两直线 |
 上一点,设P到此抛物线准线的距离是d1,到直线
上一点,设P到此抛物线准线的距离是d1,到直线 的距离是d2,则dl+d2的最小值是( )
的距离是d2,则dl+d2的最小值是( )


 是双曲线
是双曲线 的左焦点,点
的左焦点,点 是该双曲线的右顶点,过
是该双曲线的右顶点,过 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、 两点,若
两点,若 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率 的取值范围是( ).
的取值范围是( ).

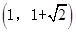

 的斜率为2且过抛物线
的斜率为2且过抛物线 的焦点F,又与
的焦点F,又与 轴交于点A,
轴交于点A, 为坐标原点,若
为坐标原点,若 的面积为4,则抛物线的方程为:
的面积为4,则抛物线的方程为: