题目内容
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,M为PA上一点,且
,M为PA上一点,且![]() ,
,
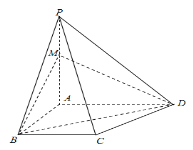
(1)证明:PC//平面MBD;
(2)若![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求直线AB与平面MBD所成角的正弦值.
,求直线AB与平面MBD所成角的正弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)连结AC交BD于N点,连结MN,可证![]() ,从而可证得
,从而可证得![]() .
.
(2)不妨设![]() ,根据四棱锥
,根据四棱锥![]() 的体积为
的体积为![]() ,解得
,解得![]() ; 利用等体积法,
; 利用等体积法,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() ,解得
,解得![]() , 可得结果.
, 可得结果.
(1)连结AC交BD于N点,连结MN,则![]() ∽
∽![]()
又![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]()
(2)不妨设![]() ,因为PA=AD=3,四棱锥
,因为PA=AD=3,四棱锥![]() 的体积为
的体积为![]() ,
,
所以![]() ,解得
,解得![]() ;
;
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
利用体积相等,![]() ,在
,在![]() 中,
中,
![]() ,
,
利用余弦定理可求得![]() ,所以
,所以![]() ,
,
所以三角形![]() 的面积
的面积![]() ,
,
代入![]() 中得:
中得:![]() ,解得
,解得![]() ,
,
又因为![]() ,所以直线AB与平面MBD所成角的正弦值为
,所以直线AB与平面MBD所成角的正弦值为![]() .
.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】某企业生产一种产品,质量测试分为:指标不小于90为一等品,不小于80小于90为二等品,小于80为三等品,每件一等品盈利50元,每件二等品盈利30元,每件三等品亏损10元,现对学徒工甲和正式工人乙生产的产品各100件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 | 5 | 15 | 35 | 35 | 7 | 3 |
乙 | 3 | 7 | 20 | 40 | 20 | 10 |
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率.
(1)求出乙生产三等品的概率;
(2)求出甲生产一件产品,盈利不小于30元的概率;
(3)若甲、乙一天生产产品分别为40件和30件,估计甲、乙两人一天共为企业创收多少元?
【题目】A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数![]() (记为t)的关系
(记为t)的关系
为: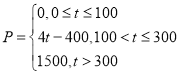 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成![]() 列联表,并判断是
列联表,并判断是
否有![]() 的把握认为A市本年度空气重度污染与供暖有关?
的把握认为A市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | p>5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 6 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2020年该地区农村居民家庭人均纯收入约为多少千元?
附:回归直线的斜率和截距的最小二乘估计公式分别为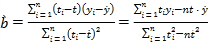 ,
,![]() .
.

