题目内容
【题目】A市积极倡导学生参与绿色环保活动，其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月（一年）内空气质量指数
进行监测，下表是在这一年随机抽取的100天的统计结果：
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
（1）若A市某企业每天由空气污染造成的经济损失P（单位：元）与空气质量指数
（记为t）的关系
为：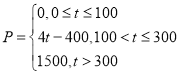
，在这一年内随机抽取一天，估计该天经济损失
元的概率；
（2）若本次抽取的样本数据有30天是在供暖季节，其中有8天为重度污染，完成
列联表，并判断是
否有
的把握认为A市本年度空气重度污染与供暖有关？
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考．
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | p>5．024 | 6．635 | 7．879 | 10．828 |
参考公式：
，其中
．
【答案】（1）P（A）=
；（2）95%的把握认为A市本年度空气重度污染与供暖有关．
【解析】
试题分析：本题第一问经济损失
元，只可能是第二段函数在此范围类，从而得到t的范围，进而通过频数统计表得到所对应的天数，利用古典概型概率公式得其概率．第二问列联表的完成只要找到各个数据所对应的含义不难完成，然后利用独立性检验相关系数看相关性大小，注意从表中查到的是出错的概率．
试题解析：（1）设“在本年内随机抽取一天，该天经济损失P∈（200，600]元”为事件A
由200＜4t﹣400≤600，得150＜t≤250，频数为39，
∴P（A）=
（2）根据以上数据得到如表：
非重度污染 | 重度污染 | 合计 | |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
合计 | 85 | 15 | 100 |
K2的观测值K2=
≈4．575＞3．841
所以有95%的把握认为A市本年度空气重度污染与供暖有关．
