Question

3．四棱锥S-ABCD，底面是矩形，SD⊥底面ABCD，AD=$\sqrt{2}$，DC=SD=2，点M在SC上，∠ABM=60°
（1）确定M点的位置，并证明你的结论
（2）求钝二面角S-AM-B的余弦值．

Answer 1

分析 （1）如图所示，建立空间直角坐标系，利用向量的夹角公式即可得出；
（2）设$\overrightarrow{n_1}（{x_1}，{y_1}，{z_1}），\overrightarrow{n_2}（{x_2}，{y_2}，{z_2}）$分别是平面SAM，MAB 一个法向量，由$\left\{\begin{array}{l}\overrightarrow{n_1}⊥\overrightarrow{MA}=0\\ \overrightarrow{n_1}⊥\overrightarrow{AS}=0\end{array}\right.且\left\{\begin{array}{l}\overrightarrow{n_2}⊥\overrightarrow{MA}=0\\ \overrightarrow{n_2}⊥\overrightarrow{AB}=0\end{array}\right.$，解出利用法向量的夹角计算公式即可得出．

解答 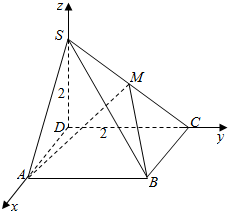解：（1）点M是线段SC的中点，证明；建立以D为原点，DA所在直线为Ox轴，DC所在直线为Oy轴，DS所在直线为Oz轴的如图空间直角坐标系：
设M（x，y，z），S（0，0，2），A$（\sqrt{2}，0，0）$，$B（\sqrt{2}，2，0）$，C（0，2，0）．
设$\overrightarrow{SM}=λ\overrightarrow{MC}$（λ＞0）．
则（x，y，z-2）=λ（-x，2-y，-z），
可得M$（0，\frac{2λ}{1+λ}，\frac{2}{1+λ}）$，
∴$\overrightarrow{MB}$=$（\sqrt{2}，\frac{2}{1+λ}，-\frac{2}{1+λ}）$，
又$\overrightarrow{AB}$=（0，2，0），∠ABM=60°．
∴cos60°=$\frac{\overrightarrow{AB}•\overrightarrow{MB}}{|\overrightarrow{AB}||\overrightarrow{MB}|}$，
∴$\frac{4}{1+λ}$=$\frac{1}{2}×2×$$\sqrt{2+（\frac{2}{1+λ}）^{2}+（-\frac{2}{1+λ}）^{2}}$，
解得λ=1，因此点M是线段SC的中点．
（2）由（1）有M（0，1，1），$\overrightarrow{MA}$=（$\sqrt{2}$，-1，-1），
又$\overrightarrow{AS}$=$（-\sqrt{2}，0，2）$，$\overrightarrow{AB}$=（0，2，0）．
设$\overrightarrow{{n}_{1}}$=（x₁，y₁，z₁），$\overrightarrow{{n}_{2}}=（{x}_{2}，{y}_{2}，{z}_{2}）$分别是平面SAM，MAB 一个法向量，
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{MA}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{AS}=0}\end{array}\right.$，解得$\overrightarrow{n}$=$（\sqrt{2}，1，1）$，
同理可得$\overrightarrow{{n}_{2}}$=$（\sqrt{2}，0，2）$．
∴cosθ=-$\frac{|\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}|}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$-\frac{\sqrt{6}}{3}$．

点评 本题考查了利用平面的法向量夹角求二面角的方法、向量的夹角公式，考查了空间想象能力、推理能力与计算能力，属于中档题．