题目内容
13．如图，在△ABC中，AD是BC边上的中线，F是AD上的一点，且$\frac{AF}{FD}$=$\frac{1}{5}$，连接CF并延长交AB于E，则$\frac{AE}{EB}$等于（ ）
| A． | $\frac{1}{12}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{10}$ |
分析 过点D作EC的平行线，得到BE的中点G，再用平行线分线段成比例定理得到AE：EG=AF：FD，然后求出AE：EB的值．
解答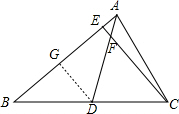 
解：如图：过点D作DG∥EC交AB于G，
∵AD是BC边上的中线，∴BD=CD，∴BG=GE．
∵DG∥EC，∴AE：EG=AF：FD=1：5．
∴AE：EB=1：10．
故选：D．
点评 本题考查的是相似三角形的判定和性质，根据题目告诉AF：FD的值，可以过点D作EC的平行线，得到BE的中点，再根据平行线分线段成比例定理得到AE：EG=AF：FD，可以求出AE：EB的值．
练习册系列答案
相关题目
四棱锥S-ABCD，底面是矩形，SD⊥底面ABCD，AD=$\sqrt{2}$，DC=SD=2，点M在SC上，∠ABM=60°
4．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点为F1（-c，0），F2（c，0），若直线y=2x与双曲线的一个交点的横坐标为c，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$+1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{3}$+$\sqrt{2}$ | D． | $\sqrt{2}$ |
如图，圆O的割线PAB交圆O于A、B两点，割线PCD经过圆心O．已知PA=AB=2$\sqrt{6}$，PO=8．则BD的长为2$\sqrt{6}$．
5．已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左右焦点分别为F1，F2，点P（$\sqrt{3}$，y0）在该双曲线上，若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，则双曲线的渐近线方程为（ ）
| A． | y=±x | B． | $y=±\sqrt{2}x$ | C． | $y=±\sqrt{3}x$ | D． | y=±2x |