Question

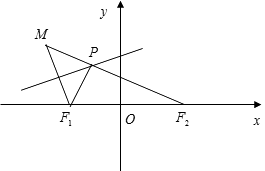
【题目】如图所示，点F1（﹣1，0），F2（1，0），动点M到点F2的距离是 ，线段MF1的中垂线交MF2于点P．

（1）当点M变化时，求动点P的轨迹G的方程；
（2）设直线l：y=kx+m与轨迹G交于M、N两点，直线F2M与F2N的倾斜角分别为α、β，且α+β=π，求证：直线l经过定点，并求该定点的坐标．

Answer 1

【答案】
（1）解：连接PF1，由 ，

∴ ，

又∵|PM|=|PF1|，∴ ，

由椭圆的定义可知2a=2 ，c=1，b=1．

即有动点P的轨迹G的方程为 ；

（2）证明：依题意 ，消去y，得

（1+2k2）x2+4kmx+2m2﹣2=0，

设M（x1，y1），N（x2，y2），

则x1+x2=﹣ ，x1x2= ，

又 = ， =

依题意得， + =0，

即 + =0，

化简得：2kx1x2+（m﹣k）（x1+x2）﹣2m=0，

∴2k +（m﹣k）（﹣ ）﹣2m=0，

整理得，m=﹣2k，

∴直线l的方程为y=k（x﹣2），

因此直线l经过定点，该定点坐标为（2，0）．

【解析】（1）连接PF1 ， 运用垂直平分线定理和椭圆的定义，可得P的轨迹为椭圆，方程为 ；（2）联立直线方程和椭圆方程，消去y，得（1+2k2）x2+4kmx+2m2﹣2=0，运用韦达定理和直线的斜率公式，化简整理，再由直线恒过定点的方法，即可得到所求定点．