题目内容
16.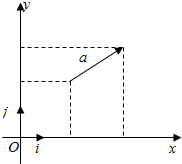 如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得
如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得$\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$…①
我们把(x,y)叫做向量$\overrightarrow{a}$的(直角)坐标,,记作$\overrightarrow{a}$=(x,y)…②
其中x叫做$\overrightarrow{a}$在x轴上的坐标,y叫做$\overrightarrow{a}$在y轴上的坐标,②式叫做向量的坐标也为(x,y).特别地,$\overrightarrow{i}$=(1,0),$\overrightarrow{j}$=(0,1),$\overrightarrow{0}$=(0,0).
如图,在直角坐标平面内,以原点O为起点作$\overrightarrow{OA}$=$\overrightarrow{a}$,则点A的位置由a唯一确定.
设$\overrightarrow{OA}=x\overrightarrow{i}+y\overrightarrow{j}$,则向量$\overrightarrow{OA}$的坐标(x,y)就是点A的坐标;反过来,点A是坐标(x,y)也是向量$\overrightarrow{OA}$的坐标.因此,在平面直角坐标系中,每一个平面向量都是可以用一对实数唯一表示.
分析 利用平面向量的坐标表示的概念直接求解.
解答  解:如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得
解:如图,在直角坐标系内,我们分别取与x轴、y轴方向相同的两个单位向量$\overrightarrow{i}$、$\overrightarrow{j}$作为基底.任作一个向量$\overrightarrow{a}$,由平面向量基本定理知,有且只有一对实数x、y,使得
$\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}$…①
我们把(x,y)叫做向量$\overrightarrow{a}$的(直角)坐标,记作$\overrightarrow{a}$=(x,y)…②
其中x叫做$\overrightarrow{a}$在x轴上的坐标,y叫做$\overrightarrow{a}$在y轴上的坐标,②式叫做向量的坐标也为(x,y).
特别地,$\overrightarrow{i}$=(1,0),$\overrightarrow{j}$=(0,1),$\overrightarrow{0}$=(0,0).
如图,在直角坐标平面内,以原点O为起点作$\overrightarrow{OA}$=$\overrightarrow{a}$,则点A的位置由a唯一确定.
设$\overrightarrow{OA}=x\overrightarrow{i}+y\overrightarrow{j}$,则向量$\overrightarrow{OA}$的坐标(x,y)就是点A的坐标;
反过来,点A是坐标(x,y)也是向量$\overrightarrow{OA}$的坐标.
因此,在平面直角坐标系中,每一个平面向量都是可以用一对实数唯一表示.
故答案为:向量$\overrightarrow{a}$的(直角)坐标,(1,0),(0,1),(0,0).
点评 本题考查平面向量的坐标表示的概念,是基础题,解题时要认真审题,熟练掌握基本概念.

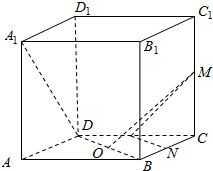 在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.
在单位正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、BC,CD的中点,O为底面ABCD的中心.