题目内容
【题目】已知直线![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对任意![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 单减,在
单减,在![]() 单增.(2)
单增.(2)![]()
【解析】
(1)求出f(x)的导数,得到f′(x),结合![]() 可解得
可解得![]() 与
与![]() 的范围,即可求出函数的单调区间.
的范围,即可求出函数的单调区间.
(2)通过讨论a的范围,得到导函数的正负,进而研究函数f(x)的单调性,求得不同情况下的函数f(x)的最小值,解出满足![]() 的a的范围即可.
的a的范围即可.
(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
,
而![]() ,且
,且![]() 在
在![]() 单调递增,所以当
单调递增,所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单减,在
单减,在![]() 单增.
单增.
(2)因为![]() ,
,![]() ,而当
,而当![]() 时,
时,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,
故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,符合题意,所以
,符合题意,所以![]() 符合题意.
符合题意.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,取
,取![]() ,则
,则![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
进而在![]() 单减,在
单减,在![]() 单增.
单增.
当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上单减,
上单减,
所以![]() .因而与题目要求在
.因而与题目要求在![]() ,
,![]() 恒成立矛盾,此类情况不成立,舍去.
恒成立矛盾,此类情况不成立,舍去.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
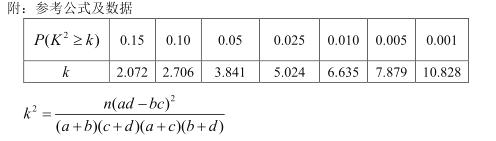
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某企业2018年招聘员工,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性 应聘人数 | 男性 录用人数 | 男性 录用比例 | 女性 应聘人数 | 女性 录用人数 | 女性 录用比例 |
| 269 | 167 |
| 40 | 24 |
|
| 40 | 12 |
| 202 | 62 |
|
| 177 | 57 |
| 184 | 59 |
|
| 44 | 26 |
| 38 | 22 |
|
| 3 | 2 |
| 3 | 2 |
|
总计 | 533 | 264 |
| 467 | 169 |
|
(1)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(2)从应聘![]() 岗位的6人中随机选择2人.记
岗位的6人中随机选择2人.记![]() 为这2人中被录用的人数,求
为这2人中被录用的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于
各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于![]() ),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() 两个品牌的共享单车在编号分别为
两个品牌的共享单车在编号分别为![]() 的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有85%的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对A品牌要从这五个城市选择三个城市进行宣传,
(ⅰ)求城市2被选中的概率;
(ⅱ)求在城市2被选中的条件下城市3也被选中的概率.