题目内容
【题目】若圆![]() 关于直线
关于直线![]() 对称,则
对称,则![]() 的最小值为__________.由点
的最小值为__________.由点![]() 向圆所作两条切线,切点记为
向圆所作两条切线,切点记为![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 外接圆的半径为__________.
外接圆的半径为__________.
【答案】 ![]()
![]()
【解析】分析:首先根据圆关于直线对称,可得直线过圆心,将圆的一般方程化为标准方程,得到圆心坐标,代入直线方程,求得![]() ,之后将其转化为关于b的关系式,配方求得最小值,通过分析图形的特征,求得什么情况下是该题所要的结果,从而得到圆心到直线的距离即为外接圆的直径,进一步求得其半径.
,之后将其转化为关于b的关系式,配方求得最小值,通过分析图形的特征,求得什么情况下是该题所要的结果,从而得到圆心到直线的距离即为外接圆的直径,进一步求得其半径.
详解:由![]() 可得
可得![]() ,
,
因为圆关于直线对称,所以圆心![]() 在直线
在直线![]() 上,
上,
即![]() ,化简得
,化简得![]() ,
,
则有![]() ,所以有
,所以有![]() 的最小值为
的最小值为![]() ;
;
根据图形的特征,可知PC最短时,对应的![]() 最小,
最小,
而PC最短时,即为C到直线![]() 的距离,
的距离,
即![]() ,此时A,B,P,C四点共圆,
,此时A,B,P,C四点共圆,
此时PC即为外接圆的直径,所以其半径就是![]() .
.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
停车距离 |
|
|
|
|
|
频数 | 24 | 42 | 24 | 9 | 1 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
(附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为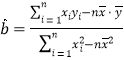 ,
,![]() )
)
