题目内容
【题目】观察以下等式:
13=12
13+23=(1+2)2
13+23+33=(1+2+3)2
13+23+33+43=(1+2+3+4)2
(1)请用含n的等式归纳猜想出一般性结论,并用数学归纳法加以证明.
(2)设数列{an}的前n项和为Sn,且an=n3+n,求S10.
【答案】(1)猜想13+23+33+…+n3=(1+2+3+…+n)2;证明见解析(2)3080
【解析】
(1)根据式子猜想出一般性结论,然后当![]() 时,证明成立,假设
时,证明成立,假设![]() 时,式子也成立,然后对
时,式子也成立,然后对![]() 时的式子进行化简,从而证明结论成立;(2)对
时的式子进行化简,从而证明结论成立;(2)对![]() 进行分组求和,然后根据(1)中所得到的求和公式,进行求和计算,得到答案.
进行分组求和,然后根据(1)中所得到的求和公式,进行求和计算,得到答案.
(1)猜想13+23+33+…+n3=(1+2+3+…+n)2;
证明:当n=1时,左边=1,右边=1,等式成立;
假设n=k时,13+23+33+…+k3=(1+2+3+…+k)2,
当n=k+1时,13+23+33+…+k3+(k+1)3=(1+2+3+…+k)2+(k+1)3
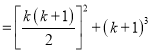
![]()
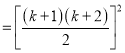
![]() ,
,
可得n=k+1时,猜想也成立,
综上可得对任意的正整数n,13+23+33+…+n3=(1+2+3+…+n)2;
(2)数列{an}的前n项和为Sn,且an=n3+n,
S10=(13+23+…+103)+(1+2+3+…+10)=(1+2+…+10)2![]()
=552+55=3080.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目