题目内容
1.函数y=$\frac{\sqrt{9-{x}^{2}}}{|x+4|+|x-3|}$( )| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,又不是偶函数 |
分析 化简函数,利用偶函数的定义判断即可.
解答 解:由9-x2≥0,可得-3≤x≤3,
∴y=f(x)=$\frac{\sqrt{9-{x}^{2}}}{|x+4|+|x-3|}$=$\frac{\sqrt{9-{x}^{2}}}{7}$,
∴f(-x)=f(x)=$\frac{\sqrt{9-{x}^{2}}}{7}$,
∴函数y=$\frac{\sqrt{9-{x}^{2}}}{|x+4|+|x-3|}$是偶函数.
故选:B.
点评 本题考查函数的奇偶性,考查学生的计算能力,正确化简函数是关键.

练习册系列答案
相关题目
11.在等差数列{an}中,S20=25,S40=100,则S60=( )
| A. | 125 | B. | 225 | C. | 150 | D. | 250 |
9.已知f(x)是R上的增函数,若a+b≥0,则有( )
| A. | f(a)+f(b)>f(-a)+f(-b) | B. | f(a)+f(b)≥f(-a)+f(-b) | C. | f(a)+f(b)<f(-a)+f(-b) | D. | f(a)+f(b)≤f(-a)+f(-b) |
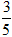 B.
B.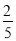 C.
C.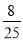 D.
D.