题目内容
1.已知$tan({α+\frac{π}{4}})=3$,求下列各式的值:(1)$\frac{{cos({π+α})-cos({\frac{π}{2}-α})}}{{sin({π-α})+sin({\frac{3π}{2}+α})}}$;
(2)sin2α-2cos2α.
分析 由$tan({α+\frac{π}{4}})=3$可求得tanα=$\frac{1}{2}$,
(1)利用诱导公式化简$\frac{cos(π+α)-cos(\frac{π}{2}-α)}{sin(π-α)+sin(\frac{3π}{2}+α)}$=$\frac{cosα+sinα}{cosα-sinα}$,再“弦”化“切”即可;
(2)利用二倍角的正弦将sin2α-2cos2α化为2sinαcosα-2cos2α,再将分母除以1=sin2α+cos2α,“弦”化“切”即可.
解答 解:∵由$tan(α+\frac{π}{4})=\frac{1+tanα}{1-tanα}$=3得tanα=$\frac{1}{2}$,于是:
(1)$\frac{cos(π+α)-cos(\frac{π}{2}-α)}{sin(π-α)+sin(\frac{3π}{2}+α)}$=$\frac{-cosα-sinα}{sinα-cosα}$=$\frac{cosα+sinα}{cosα-sinα}$=$\frac{1+tanα}{1-tanα}$=3;
(2)sin2α-2cos2α=2sinαcosα-2cos2α=$\frac{2sinαcosα-2{cos}^{2}α}{{sin}^{2}α+{cos}^{2}α}$=$\frac{2tanα-2}{{tan}^{2}α+1}$=-$\frac{4}{5}$.
点评 本题考查同角三角函数基本关系式及变形公式的应用,利用诱导公式及sin2α+cos2α=1实现角α的正弦、余弦的互化、利用tanα可以实现角α的弦切互化是关键,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
11.已知集合M={x|0<x<1},N={x|x=t2+2t+3},则(∁NM)∩N=( )
| A. | {x|0<x<1} | B. | {x|x>1} | C. | {x|x≥2} | D. | {x|1<x<2} |
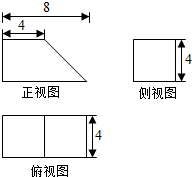 已知某几何体的三视图如下,请画出它的直观图(单位:cm)
已知某几何体的三视图如下,请画出它的直观图(单位:cm)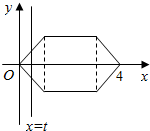 如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6
如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6