题目内容
已知圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称.
(I)求m的值;
(Ⅱ)直线l与圆C交于A,B两点,
•
=-3(O为坐标原点),求圆C的方程.
(I)求m的值;
(Ⅱ)直线l与圆C交于A,B两点,
| OA |
| OB |
(I)x2+y2+2x+a=0⇒(x+1)2+y2=1-a,圆心(-1,0).
∵圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称,∴直线过圆心,
∴-m+0+1=0⇒m=1,
故m的值为1.
(II)设A(x1,y1),B(x2,y2)
•
=x1x2+y1y2=2x1x2+x1+x2+1
⇒2x2+4x+1+a=0,
根据韦达定理:x1+x2=-2;x1x2=
.
∴1+a-2+1=-3⇒a=-3.
∴圆C的方程是:(x+1)2+y2=4.
∵圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称,∴直线过圆心,
∴-m+0+1=0⇒m=1,
故m的值为1.
(II)设A(x1,y1),B(x2,y2)
| OA |
| OB |
|
根据韦达定理:x1+x2=-2;x1x2=
| 1+a |
| 2 |
∴1+a-2+1=-3⇒a=-3.
∴圆C的方程是:(x+1)2+y2=4.

练习册系列答案
相关题目
 中,
中,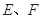 分别是腰
分别是腰 的中点,
的中点, 在线段
在线段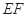 上,且
上,且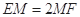 ,下底是上底的2倍,若
,下底是上底的2倍,若 ,用
,用 表示
表示 .
.
