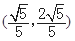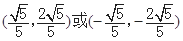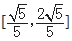题目内容

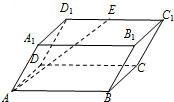
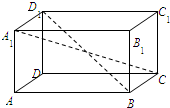
如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AA1=3，∠BAA1=60°，E为棱C1D1的中点，则
AB
•
AE
=______．
由题意可得
AE
=
AD
+
DD1
+
D1E

=
AD
+
AA1
+
1
2
AB
，
∴
AB
•
AE
=
AB
•（
AD
+
AA1
+
1
2
AB
）
=
AB
•
AD
+
AB
•
AA1
+
1
2
AB
2
=0+4×3×cos60°+
1
2
×42
=14
故答案为：14
练习册系列答案
相关题目
已知
a
与
b
的夹角是60°，
a
=（2，0），
b
=（sinθ，cosθ），则|
a
+2
b
|=______．
在平面直角坐标系xOy中，已知四边形OABC是等腰梯形，A(6，0)，C(1，
3
)，点，M满足
OM
=
1
2
OA
，点P在线段BC上运动（包括端点），如图．
（1）求∠OCM的余弦值；
（2）是否存在实数λ，使(
OA
-λ
OP
)⊥
CM
，若存在，求出满足条件的实数λ的取值范围，若不存在，请说明理由．
如图，在长方体ABCD-A1B1C1D1中，设AD=AA1=1，AB=2，则|
CC1
-
BD1|
|=______，
CC1
•
CA1|
=______．
如图，已知F1、F2是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则
PF1
•
PF2
=______；椭圆C的离心率为______．
设F1、F2分别是椭圆
x2
4
+y2=1的左、右焦点．
（Ⅰ）若P是第一象限内该椭圆上的一点，且
PF1
•
PF2
=-
5
4
，求点P的作标；
（Ⅱ）设过定点M（0，2）的直线l与椭圆交于不同的两点A、B，且∠AOB为锐角（其中O为作标原点），求直线l的斜率k的取值范围．
已知圆C：x2+y2+2x+a=0上存在两点关于直线l：mx+y+1=0对称．
（I）求m的值；
（Ⅱ）直线l与圆C交于A，B两点，
OA
•
OB
=-3（O为坐标原点），求圆C的方程．
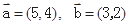已知，则与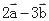平行的单位向量为(   ).
A．B．
C．D．
向量
a
=（3，4），
b
=（-4，3），则
a
•
b
=（　　）
A．0B．（-12，12）C．25D．90°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网