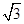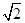题目内容
已知△ABC中，
⊥
，|
-
|=2，点M是线段BC（含端点）上的一点，且
•(
+
)=1，则|
|的取值范围是______．
| AB |
| AC |
| AB |
| AC |
| AM |
| AB |
| AC |
| AM |
如图所示，建立直角坐标系．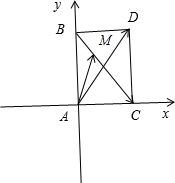
设B（0，c），C（b，0），D（b，c），M（x，y）．
∵|
-
|=|
|=2，
∴b2+c2=4．
∵
+
=
，
∴
•(
+
)=
•
=（x，y）•（b，c）=bx+cy=1．
|
|=
，
∵（x2+y2）（b2+c2）≥（bx+cy）2，
∴4（x2+y2）≥1，
∴
≥
，即|
|≥
．
又
+
=1，
∴1=（bx+cy）(
+
)=x2+y2+
+
，
∵b＞0，c＞0，x≥0，y≥0．
∴x2+y2≤1，即
≤1．（当且仅当x=0或y=0时取等号）．
综上可知：
≤|
|≤1．
故答案为：[
，1]．
设B（0，c），C（b，0），D（b，c），M（x，y）．
∵|
| AB |
| AC |
| CB |
∴b2+c2=4．
∵
| AB |
| AC |
| AD |
∴
| AM |
| AB |
| AC |
| AM |
| AD |
|
| AM |
| x2+y2 |
∵（x2+y2）（b2+c2）≥（bx+cy）2，
∴4（x2+y2）≥1，
∴
| x2+y2 |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
又
| x |
| b |
| y |
| c |
∴1=（bx+cy）(
| x |
| b |
| y |
| c |
| cxy |
| b |
| bxy |
| c |
∵b＞0，c＞0，x≥0，y≥0．
∴x2+y2≤1，即
| x2+y2 |
综上可知：
| 1 |
| 2 |
| AM |
故答案为：[
| 1 |
| 2 |
练习册系列答案
相关题目
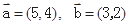，则与
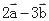平行的单位向量为( ).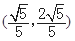
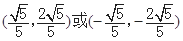
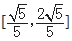
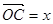
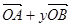，则x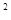
+y的最小值等于.( )
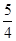B.1 C.
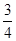D.
＋
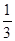
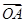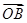＋2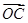
＝0，则△ABC的面积与△AOC的面积的比值为( )
