题目内容
10．设集合M={x|y=$\sqrt{2-x}$+2}，N={y|y=$\sqrt{2-x}$+2}，则A∩B={2}．分析 求出M中x的范围确定出M，求出N中y的范围确定出N，找出两集合的交集即可．
解答 解：由y=$\sqrt{2-x}$+2，得到2-x≥0，即x≤2，
∴M={x|x≤2}，
由N中y=$\sqrt{2-x}$+2≥2，得到B={y|y≥2}，
则A∩B={2}，
故答案为：{2}．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．执行如图所示的程序框图，如果输入m=30，n=18，则输出的m的值为（ ）
| A． | 0 | B． | 6 | C． | 12 | D． | 18 |
18．已知双曲线C：$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左、右焦点分别为F1、F2，P为C的右支上一点，且|PF2|=|F1F2|，则cos∠F1F2P等于（ ）
| A． | $\frac{7}{9}$ | B． | -$\frac{5}{6}$ | C． | -$\frac{7}{18}$ | D． | 1 |
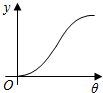
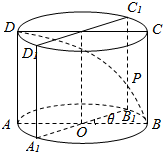已知圆柱OO1底面半径为1，高为π，ABCD是圆柱的一个轴截面．动点M从点B出发沿着圆柱的侧面到达点D，其距离最短时在侧面留下的曲线Γ如图所示．现将轴截面ABCD绕着轴OO1逆时针旋转θ（0＜θ≤π）后，边B1C1与曲线Γ相交于点P，设BP的长度为f（θ），则y=f（θ）的图象大致为（ ）
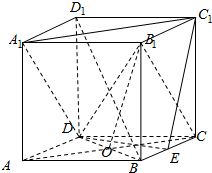已知正方体ABCD-A1B1C1D1，底面ABCD的中心为O，E为BC的中点，如图