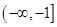题目内容
设 在区间
在区间 上有定义, 若
上有定义, 若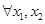
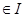 , 都有
, 都有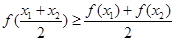 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若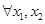
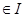 , 都有
, 都有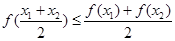 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若 是区间
是区间 的向上凸函数,则
的向上凸函数,则 是区间
是区间 的向下凸函数;
的向下凸函数;
②若 和
和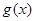 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则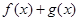 是区间
是区间 的向上凸函数;
的向上凸函数;
③若 在区间
在区间 的向下凸函数且
的向下凸函数且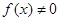 ,则
,则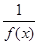 是区间
是区间 的向上凸函数;
的向上凸函数;
④若 是区间
是区间 的向上凸函数,
的向上凸函数,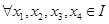 , 则有
, 则有
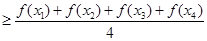
其中正确的结论个数是( )
 在区间
在区间 上有定义, 若
上有定义, 若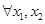
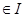 , 都有
, 都有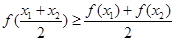 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若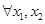
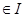 , 都有
, 都有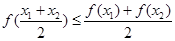 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:①若
 是区间
是区间 的向上凸函数,则
的向上凸函数,则 是区间
是区间 的向下凸函数;
的向下凸函数;②若
 和
和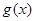 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则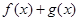 是区间
是区间 的向上凸函数;
的向上凸函数;③若
 在区间
在区间 的向下凸函数且
的向下凸函数且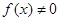 ,则
,则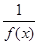 是区间
是区间 的向上凸函数;
的向上凸函数;④若
 是区间
是区间 的向上凸函数,
的向上凸函数,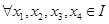 , 则有
, 则有
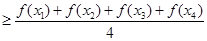
其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
①②
试题分析:利用定义易知正确,③反例
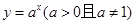
因为
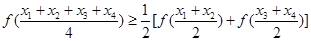
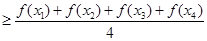 所以④正确.故填写①②。
所以④正确.故填写①②。点评:主要是对于新定义的理解和运用,属于中档题。

练习册系列答案
相关题目
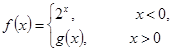 若
若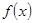 是奇函数,则
是奇函数,则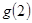 的值是( )
的值是( )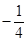
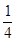
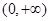 ,若对给定的正数K,定义
,若对给定的正数K,定义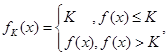 则当函数
则当函数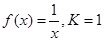 时,
时, 
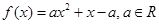 .
.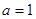 ,解不等式
,解不等式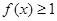 ;
;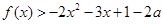 对一切实数
对一切实数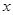 恒成立,求实数
恒成立,求实数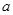 的取值范围;
的取值范围;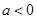 ,解不等式
,解不等式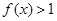 .
.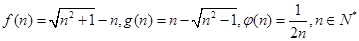 ,则
,则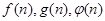 的大小关系
的大小关系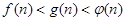

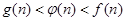
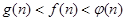
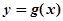 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为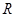 的函数
的函数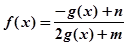 是奇函数。
是奇函数。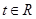 ,不等式
,不等式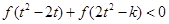 恒成立,求实数
恒成立,求实数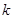 的取值范围
的取值范围
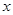 的不等式
的不等式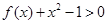
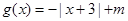 ,
,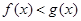 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围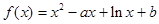
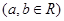 ,
,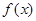 在
在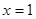 处的切线方程为
处的切线方程为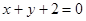 ,求实数
,求实数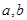 的值;
的值; 的取值范围.
的取值范围.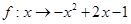 是集合
是集合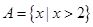 到集合
到集合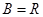 的映射。若对于实数
的映射。若对于实数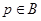 ,在
,在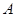 中不存在对应的元素,则实数
中不存在对应的元素,则实数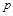 的取值范围是( )
的取值范围是( )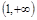 B.
B. 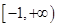 C.
C. 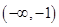 D.
D.