题目内容
已知指数函数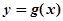 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为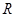 的函数
的函数
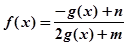 是奇函数。
是奇函数。
(1)确定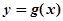 的解析式;(2)求m,n的值;
的解析式;(2)求m,n的值;
(3)若对任意的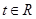 ,不等式
,不等式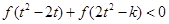 恒成立,求实数
恒成立,求实数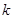 的取值范围
的取值范围
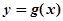 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为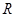 的函数
的函数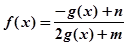 是奇函数。
是奇函数。(1)确定
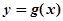 的解析式;(2)求m,n的值;
的解析式;(2)求m,n的值;(3)若对任意的
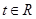 ,不等式
,不等式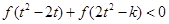 恒成立,求实数
恒成立,求实数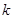 的取值范围
的取值范围(1)m=2,n=1(2)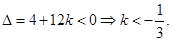
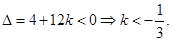
试题分析:解:(1)
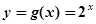 2分
2分(2)由(1)知:
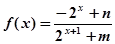
因为
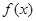 是奇函数,所以
是奇函数,所以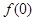 =0,即
=0,即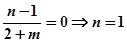
∴
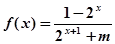 , 又由f(1)= -f(-1)知
, 又由f(1)= -f(-1)知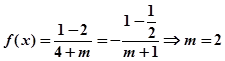 3分
3分(3)由(2)知
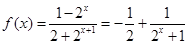 ,
,易知
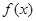 在
在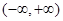 上为减函数。
上为减函数。又因
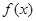 是奇函数,从而不等式:
是奇函数,从而不等式: 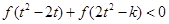 等价于
等价于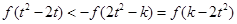 ,
,因
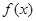 为减函数,由上式推得:
为减函数,由上式推得: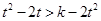
即对一切
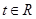 有:
有: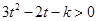 ,
,从而判别式
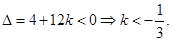 5分
5分点评:主要是考查了函数的奇偶性和单调性的性质的综合运用,结合概念来判定,并解不等式,属于中档题。

练习册系列答案
相关题目
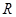 上的函数
上的函数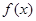 满足
满足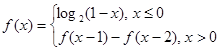 ,则
,则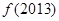 的值为_______________.
的值为_______________.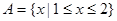 ,
,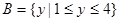 ,则下述对应法则
,则下述对应法则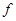 中,不能构成A到B的映射的是( )
中,不能构成A到B的映射的是( )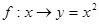
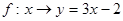

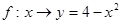
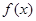 在
在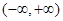 为奇函数,
为奇函数,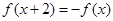 ,当
,当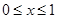 时,
时,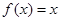 ,则
,则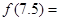 。
。 在区间
在区间 上有定义, 若
上有定义, 若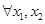
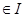 , 都有
, 都有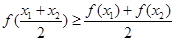 , 则称
, 则称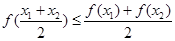 , 则称
, 则称 是区间
是区间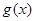 都是区间
都是区间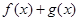 是区间
是区间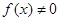 ,则
,则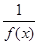 是区间
是区间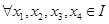 , 则有
, 则有
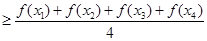
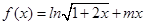 .
.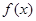 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数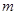 的取值范围;
的取值范围;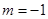 时,求函数
时,求函数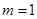 时,且
时,且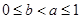 ,证明:
,证明: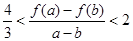 .
.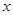 小时的收费为
小时的收费为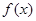 元
元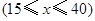 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动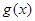 元
元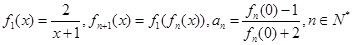
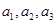 ,并求数列
,并求数列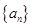 的通项公式.
的通项公式. 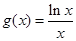 在
在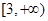 上为减函数,设数列
上为减函数,设数列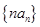 的前
的前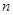 的和为
的和为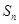 ,
,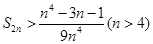
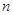 个月的维修费为
个月的维修费为 元,买这种冰激凌机花费
元,买这种冰激凌机花费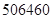 元,使用
元,使用 年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( )
年报废,那么这台冰激凌机从投入使用到报废,每天的消耗是( ) 机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;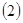 一年按
一年按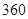 天计算.)
天计算.)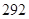 元
元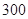 元
元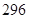 元
元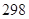 元
元