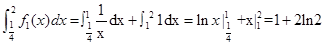题目内容
设函数y=f(x)的定义域为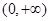 ,若对给定的正数K,定义
,若对给定的正数K,定义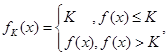 则当函数
则当函数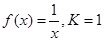 时,
时, 
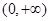 ,若对给定的正数K,定义
,若对给定的正数K,定义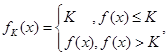 则当函数
则当函数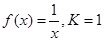 时,
时, 
2ln2+1
试题分析:因为函数
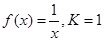 ,
,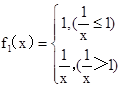 ,即
,即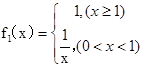 f1(x)=
f1(x)=所以,
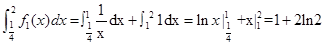
点评:中档题,在理解题意的基础上,确定分段函数的解析式,并对分段函数进行定积分计算。

练习册系列答案
相关题目
题目内容
 ,若对给定的正数K,定义
,若对给定的正数K,定义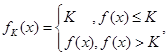 则当函数
则当函数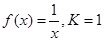 时,
时, 
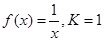 ,
,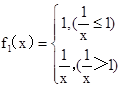 ,即
,即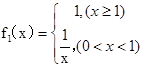 f1(x)=
f1(x)=