题目内容
在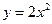 上有一点
上有一点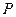 ,它到
,它到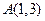 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点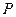 的坐标是( )
的坐标是( )
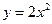 上有一点
上有一点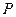 ,它到
,它到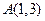 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点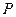 的坐标是( )
的坐标是( )| A.(-2,1) | B.(1,2) | C.(2,1) | D.(-1,2) |
B
略

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
题目内容
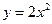 上有一点
上有一点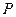 ,它到
,它到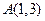 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点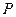 的坐标是( )
的坐标是( )| A.(-2,1) | B.(1,2) | C.(2,1) | D.(-1,2) |

 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案