题目内容
3.已知n∈N*,且n>1,三个数ln$\frac{n+1}{n}$、$\frac{1}{n+1}$、$\frac{1}{n}$的大小关系是( )| A. | $\frac{1}{n}$>ln$\frac{n+1}{n}$>$\frac{1}{n+1}$ | B. | ln$\frac{n+1}{n}$>$\frac{1}{n}$>$\frac{1}{n+1}$ | C. | $\frac{1}{n}$>$\frac{1}{n+1}$>ln$\frac{n+1}{n}$ | D. | $\frac{1}{n+1}$>$\frac{1}{n}$>ln$\frac{n+1}{n}$ |
分析 构造函数f(x)=x-ln(1+x),x>0,利用导数判断f(x)的单调性,得出x>ln(1+x),令x=$\frac{1}{n}$得$\frac{1}{n}$>ln$\frac{n+1}{n}$;同理,设g(x)=ln(1+x)-$\frac{x}{1+x}$,x>0,得出ln$\frac{n+1}{n}$>$\frac{1}{n+1}$,即得$\frac{1}{n}$>ln$\frac{n+1}{n}$>$\frac{1}{n+1}$.
解答 解:设函数f(x)=x-ln(1+x),x>0,
∴f′(x)=1-$\frac{1}{1+x}$>0,
∴f(x)在(0,+∞)上是增函数,
∴f(x)>f(0)=0,
∴x>ln(1+x);
令x=$\frac{1}{n}$,n∈N*,且n>1,
则$\frac{1}{n}$>ln(1+$\frac{1}{n}$)=ln$\frac{n+1}{n}$;
同理,设g(x)=ln(1+x)-$\frac{x}{1+x}$,x>0,
∴g′(x)=$\frac{1}{1+x}$-$\frac{1}{{(1+x)}^{2}}$=$\frac{x}{{(1+x)}^{2}}$>0,
∴g(x)在(0,+∞)上是增函数,
∴g(x)>g(0)=0,
∴ln(1+x)>$\frac{x}{1+x}$;
令x=$\frac{1}{n}$,n∈N*,且n>1,
∴ln(1+$\frac{1}{n}$)>$\frac{\frac{1}{n}}{1+\frac{1}{n}}$,
即ln$\frac{n+1}{n}$>$\frac{1}{n+1}$;
综上,$\frac{1}{n}$>ln$\frac{n+1}{n}$>$\frac{1}{n+1}$.
故选:A.
点评 本题考查了构造函数的应用问题,也考查了利用导数判断函数的单调性以及利用函数的单调性比较大小的应用问题,是综合性题目.

| A. | $-\frac{3}{2}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
(1)能否在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关系?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中数学、物理两科成绩至少有一科优秀的次数为X,求X的期望E(X).
附:
| K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
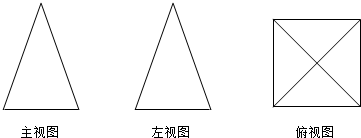
| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 四棱锥 |
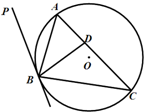 如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA.若AD=2,AC=8,则AB=4.
如图所示,直线PB与圆O相切于点B,D是弦AC上的点,∠PBA=∠DBA.若AD=2,AC=8,则AB=4.