题目内容
14.点O在△ABC内部且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow 0$,则△ABC的面积与△BOC的面积之比是( )| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | 4 |
分析 根据向量的运行性质结合三角形重心的性质,易得是△ABC的重心,结合三角形的面积性质进行求解.
解答 解:由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow 0$,
则$\overrightarrow{OA}$+$\overrightarrow{OB}$=-$\overrightarrow{OC}$=$\overrightarrow{CO}$,
取AB的中点E,以OA,OB为边作平行四边形OADB,
则$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OD}$=2$\overrightarrow{OE}$,
∴$\overrightarrow{CO}$=2$\overrightarrow{OE}$,
则O是△ABC的重心,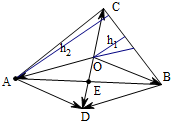
由重心的性质,可得O到BC的距离为A到BC距离的$\frac{1}{3}$,
即△OBC的面积为△ABC的面积$\frac{1}{3}$,
则∴S△ABC:S△OBC=3:1.
故选:C
点评 本题考查向量在几何中的应用,注意由向量关系式推出O是三角形的重心,结合三角形的重心的性质是解决本题的关键.

练习册系列答案
相关题目
9.设等差数列{an}的前n项和为sn,则s4,s8-s4,s12-s8,s16-s12成等差数列.类比以上结论有:设等比数列{bn}前n项积为Tn,则T4,( ),$\frac{{{T_{16}}}}{{{T_{12}}}}$成等比数列.
| A. | $\frac{T_6}{T_4},\frac{{{T_{12}}}}{T_6}$ | B. | $\frac{T_8}{T_4},\frac{{{T_{12}}}}{T_8}$ | ||
| C. | $\frac{{{T_{10}}}}{T_4},\frac{{{T_{12}}}}{{{T_{10}}}}$ | D. | $\frac{{{T_{16}}}}{T_4},\frac{{{T_{12}}}}{{{T_{16}}}}$ |
3.下列角的终边与37°角的终边在同一直线上的是( )
| A. | -37° | B. | 143° | C. | 379° | D. | -143° |
4.过点(5,3)且与直线x-2y-2=0垂直的直线方程是( )
| A. | x+2y-11=0 | B. | 2x+y-13=0 | C. | 2x-y-7=0 | D. | x-2y+1=0 |