题目内容
20.已知正方体ABCD-A1B1C1D1的棱长为1,且点E为棱AB上任意一个动点.当点B1到平面A1EC的距离为$\frac{{\sqrt{21}}}{6}$时,点E所有可能的位置有几个2.分析 建立如图所示空间直角坐标系,设出E点坐标,利用B1到平面A1EC的距离为$\frac{{\sqrt{21}}}{6}$求得a的值得答案.
解答 解:建立如图所示的空间直角坐标系,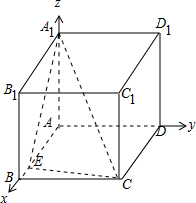
设E(a,0,0),C(1,1,0),A1(0,0,1),B1(1,0,1).
则$\overrightarrow{{A}_{1}C}=(1,1,-1)$,$\overrightarrow{{A}_{1}E}=(a,0,-1)$,
设平面A1EC的一个法向量为$\overrightarrow{n}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}C}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}E}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x+y-z=0}\\{ax-z=0}\end{array}\right.$,取z=a,则x=1,y=a-1.
∴$\overrightarrow{n}=(1,a-1,a)$.
$\overrightarrow{{A}_{1}{B}_{1}}=(1,0,0)$,
由$\frac{|\overrightarrow{{A}_{1}{B}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}=\frac{1}{\sqrt{1+{a}^{2}+(a-1)^{2}}}=\frac{\sqrt{21}}{6}$,解得:$a=\frac{7±\sqrt{21}}{14}$.
∴E所有可能的位置有2个.
故答案为:2.
点评 本题考查多面体中的点线面间的距离,考查了空间向量在解立体几何问题中的应用,是中档题.

 名校课堂系列答案
名校课堂系列答案(1)m为何值时,三线共点;
(2)m=0时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,m的取值范围.
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
| A. | ∅ | B. | S | C. | T | D. | {0,1} |
 如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2$\sqrt{2}$m | B. | 2$\sqrt{3}$m | C. | 4 m | D. | 6 m |

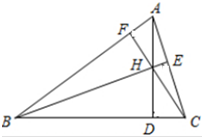 如图,已知△ABC的三条高是AD,BE,CF,用向量方法证明:AD,BE,CF相交于一点.
如图,已知△ABC的三条高是AD,BE,CF,用向量方法证明:AD,BE,CF相交于一点.