题目内容
12. 如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )
如图,一隧道截面由一个长方形和抛物线构成现欲在随道抛物线拱顶上安装交通信息采集装置若位置C对隧道底AB的张角θ最大时采集效果最好,则采集效果最好时位置C到AB的距离是( )| A. | 2√2√2m | B. | 2√3√3m | C. | 4 m | D. | 6 m |
分析 建立如图所示的坐标系,求出抛物线的方程,设C(x,y)(y>-6),由A(-3,-6),B(3,-6),可得kCA=y+6x+4y+6x+4,kCB=y+6x−4y+6x−4,求出tan∠BCA,利用基本不等式,即可得出结论.
解答  解:建立如图所示的坐标系,设抛物线方程为x2=-2py(p>0),
解:建立如图所示的坐标系,设抛物线方程为x2=-2py(p>0),
将点(4,-4)代入,可得p=2,
所以抛物线方程为x2=-4y,
设C(x,y)(y>-6),则
由A(-4,-6),B(4,-6),可得kCA=y+6x+4y+6x+4,kCB=y+6x−4y+6x−4,
∴tan∠BCA=y+6x+4−y+6x−41+y+6x+4•y+6x−4y+6x+4−y+6x−41+y+6x+4∙y+6x−4=−8(y+6)x2−16+(y+6)2=−8(y+6)y2+8y+20,
令t=y+6(t>0),则tan∠BCA=−8tt2−4t+8=−8t+8t−4≥−84√2−4
∴t=2√2时,位置C对隧道底AB的张角最大,
故选:A.
点评 本题考查抛物线的方程与应用,考查基本不等式,确定抛物线的方程及tan∠BCA,正确运用基本不等式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )
如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )
 如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )
如图所示的是一多面体的三视图(尺寸如图所示,单位:cm),则它的表面积是( )| A. | (6+3√3)cm2 | B. | (12+3√3)cm2 | C. | 15cm2 | D. | 9cm2 |
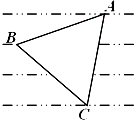 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2