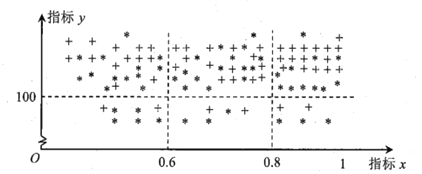
题目内容
【题目】如图所示的几何体中,四边形![]() 为正方形,AD∥B
为正方形,AD∥B![]() ,平面ABC⊥平面BC
,平面ABC⊥平面BC![]() ,AB=AC=
,AB=AC=![]() ,AD=1,∠ABC=45°。
,AD=1,∠ABC=45°。

(1)求证:AB⊥CD;
(2)求点C到平面D![]() 的距离。
的距离。
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)三角形ABC中可得![]() ;由题意可得
;由题意可得![]() ,进而
,进而![]() ,故得
,故得![]() ,于是可证得
,于是可证得![]() .(2)取BC的中点O,
.(2)取BC的中点O, ![]() 的中点M,
的中点M,
连接DO,DM,OM.在三角形DOM中,可证得![]() ;在三角形
;在三角形![]() 中,可得
中,可得![]() ,故可得
,故可得![]() ,于是得
,于是得![]() ,从而得到
,从而得到![]() ,又由
,又由![]() 得点C到平面
得点C到平面![]() 的距离为
的距离为![]()
试题解析:
(1)证明:在三角形ABC中, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
又![]()
![]()
![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
又![]()
![]()
![]() ,
,
∴![]()
(2)解:如 图,取BC的中点O, ![]() 的中点M,连接DO,DM,OM,
的中点M,连接DO,DM,OM,

在三角形DOM中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
又在三角形![]() 中,
中, ![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
∵![]() ,
,
∴点C到平面![]() 的距离为
的距离为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目