Question

【题目】已知斜三棱柱的所有棱长都相等，且.

(1)求证：；

(2)直线与直线所成角的余弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）通过△和△为等边三角形，可得从而得BC⊥平面A1AD，得到A1A⊥BC；

（2）利用异面直线所成角的定义作出，找到直线与直线所成角，在△中利用余弦定理求解即可.

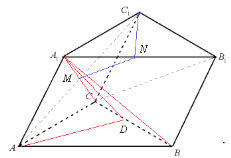
（1）连接,取线段的中点为，再连接.

∵ 三棱柱的所有棱长相等，且

∴ △和△为等边三角形

∵ 为上述两个三角形公共边的中点

∴

∵平面，

∴ 平面

∵平面

∴

(2)连接交于点M,取线段的中点为N，再连接.不妨设棱长为2.

由得,因而四边形为正方形,.

∵ 分别为△的边的中点

∴, ∴即为直线与直线所成角，

，

同（1）可知△和△为等边三角形，.

在△中，

所以，直线与直线所成角的余弦值.