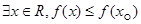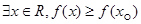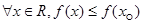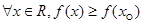题目内容
已知圆 的极坐标方程为
的极坐标方程为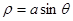 ,则“
,则“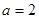 ”是“圆
”是“圆 与极轴所在直线相切”的 ( )
与极轴所在直线相切”的 ( )
| A.充分不必要条件. | B.必要不充分条件. |
| C.充要条件. | D.既不充分又不必要条件. |
A
解析试题分析:根据题意,圆 的极坐标方程为
的极坐标方程为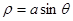 ,可知圆心为(0,
,可知圆心为(0,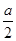 ),半径为
),半径为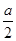 的圆,而a=2则说明圆心为(0,1),半径为1,显然与坐标轴相切,满足充分性,但是反之,a=-2也成立,故不是必要条件,因此充分不必要条件.选A
的圆,而a=2则说明圆心为(0,1),半径为1,显然与坐标轴相切,满足充分性,但是反之,a=-2也成立,故不是必要条件,因此充分不必要条件.选A
考点:圆的极坐标方程
点评:解决的关键是根据极坐标化为直角坐标方程,利用直线与圆的位置关系来判定,属于解题。

练习册系列答案
相关题目
下列说法错误的是( )
A.命题:“已知 是 是 上的增函数,若 上的增函数,若 ,则 ,则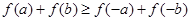 ”的逆否命题为真命题 ”的逆否命题为真命题 |
B.命题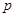 :“存在 :“存在 ,使得 ,使得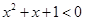 ”,则 ”,则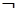 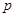 :“任意 :“任意 ,均有 ,均有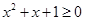 ” ” |
C.若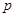 且 且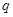 为假命题,则 为假命题,则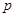 、 、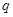 均为假命题 均为假命题 |
D.“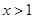 ”是“ ”是“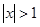 ”的充分不必要条件 ”的充分不必要条件 |
给出如下四个命题:
①若“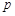 且
且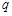 ”为假命题,则
”为假命题,则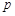 、
、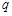 均为假命题;
均为假命题;
②命题“若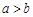 ,则
,则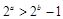 ”的否命题为“若
”的否命题为“若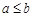 ,则
,则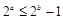 ”;
”;
③“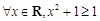 ”的否定是“
”的否定是“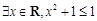 ”;
”;
④等比数列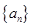 中,首项
中,首项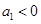 ,则数列
,则数列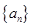 是递减数列的充要条件是公比
是递减数列的充要条件是公比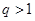 ;
;
其中不正确的命题个数是
| A.4 | B.3 | C.2 | D.1 |
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若△ABC不是等腰三角形,则它的任何两个内角不相等.”的逆否命题是( )
| A.“若△ABC是等腰三角形,则它的任何两个内角相等” |
| B.“若△ABC任何两个内角不相等,则它不是等腰三角形” |
| C.“若△ABC有两个内角相等,则它是等腰三角形” |
| D.“若△ABC任何两个角相等,则它是等腰三角形” |
对于任意实数 ,<
,< >表示不小于
>表示不小于 的最小整数,例如<1.1>=2,<
的最小整数,例如<1.1>=2,<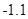 >=
>= 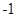 ,那么“
,那么“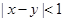 ”是“<
”是“< >=<
>=<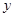 >”( ).
>”( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“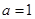 ”是“直线
”是“直线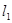 :
: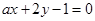 与
与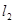 :
: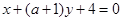 平行”的【 】.
平行”的【 】.
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题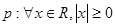 ,则
,则 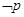 是
是
A.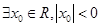 | B.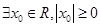 |
C.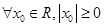 | D.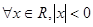 |
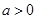 ,函数
,函数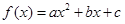 ,若
,若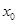 满足关于
满足关于 的方程
的方程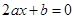 ,则下列选项的命题中为假命题的是( )
,则下列选项的命题中为假命题的是( )