题目内容
在△ABC中,∠B=45°,b=
,cosC=
.
(1)求a;
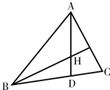
(2)设AB的中点为D,求中线CD的长.
| 10 |
2
| ||
| 5 |
(1)求a;
(2)设AB的中点为D,求中线CD的长.
(1)∵cosC=
,∴sinC=
=

可得sinA=sin(B+C)=sinBcosC+cosBsinC=
•
+
•
=
由正弦定理
=
,得a=
=
=3
;
(2)∵由余弦定理,得c2=a2+b2-2abcosC
∴c2=18+10-2×3
×
×
=4,可得c=2
设中线CD=x,则有
∵AB2+(2CD)2=2(BC2+AC2),即c2+4x2=2(a2+b2)
∴4x2=2(a2+b2)-c2=2(18+10)-4=52,解之得x=
即AB边的中线CD的长等于
.
2
| ||
| 5 |
| 1-cos2C |
| ||
| 5 |

可得sinA=sin(B+C)=sinBcosC+cosBsinC=
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
3
| ||
| 10 |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
| ||||||
|
| 2 |
(2)∵由余弦定理,得c2=a2+b2-2abcosC
∴c2=18+10-2×3
| 2 |
| 10 |
2
| ||
| 5 |
设中线CD=x,则有
∵AB2+(2CD)2=2(BC2+AC2),即c2+4x2=2(a2+b2)
∴4x2=2(a2+b2)-c2=2(18+10)-4=52,解之得x=
| 13 |
即AB边的中线CD的长等于
| 13 |

练习册系列答案
相关题目
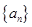 中,
中,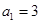 ,前
,前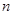 项和
项和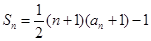 .
.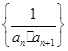 的前
的前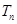 ,是否存在实数
,是否存在实数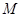 ,使得
,使得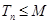 对一切正整数
对一切正整数