题目内容
【题目】已知![]() 且
且![]() ,函数
,函数![]() ,
,![]() .
.
(1)指出![]() 的单调性(不要求证明);
的单调性(不要求证明);
(2)若有![]() 求
求![]() 的值;
的值;
(3)若![]() ,求使不等式
,求使不等式![]() 恒成立的
恒成立的![]() 的取值范围.
的取值范围.
【答案】(1)![]() 上的减函数;(2)
上的减函数;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对![]() 分类讨论,然后说明函数的单调性;
分类讨论,然后说明函数的单调性;
(2)构造新函数![]() ,说明
,说明![]() 的奇偶性,再根据已知条件即可计算出
的奇偶性,再根据已知条件即可计算出![]() 的值;
的值;
(3)根据![]() 的奇偶性,将不等式变形,再根据
的奇偶性,将不等式变形,再根据![]() 的单调性即可将函数值的大小关系转变为自变量间的大小关系,再利用二次函数的
的单调性即可将函数值的大小关系转变为自变量间的大小关系,再利用二次函数的![]() 求解出结果.
求解出结果.
(1)![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是减函数,所以
是减函数,所以![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,
,![]() 是增函数,所以
是增函数,所以![]() 是减函数,
是减函数,
综上可知:![]() 是
是![]() 上的减函数;
上的减函数;
(2)令![]() ,因为
,因为![]() ,所以
,所以![]() 是奇函数,
是奇函数,
又因为![]() 即
即![]() 也是奇函数,所以
也是奇函数,所以![]() 是
是![]() 上的奇函数,
上的奇函数,
所以![]() ,所以
,所以![]() ,
,
所以![]() ;
;
(3)![]() ,因为
,因为![]() 与
与![]() 均是
均是![]() 上的减函数和奇函数,
上的减函数和奇函数,
所以![]() 也是
也是![]() 上的减函数和奇函数,
上的减函数和奇函数,
又因为![]() 恒成立,所以
恒成立,所以![]() 恒成立,
恒成立,
所以![]() 恒成立,所以
恒成立,所以![]() 恒成立,所以
恒成立,所以![]() ,
,
所以![]() .
.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】(2016·郑州模拟)某市公安局为加强安保工作,特举行安保项目的选拔比赛活动,其中A、B两个代表队进行对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式进行三场比赛,每场胜队得1分,负队得0分,设A队、B队最后所得总分分别为ξ,η,且ξ+η=3.
对阵队员 | A队队员胜 | A队队员负 |
A1对B1 |
|
|
A2对B2 |
|
|
A3对B3 |
|
|
(1)求A队最后所得总分为1的概率;
(2)求ξ的分布列,并用统计学的知识说明哪个队实力较强.
【题目】某大型高端制造公司为响应(中国制造2025)中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:
月份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用 | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
(1)根据数据可知![]() 与
与 ![]() 之间存在线性相关关系.
之间存在线性相关关系.
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到0.001);
的线性回归方程(系数精确到0.001);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方估计当月产品的销量;
(2)为庆祝该公司9月份成立30周年,特制定以下奖励制度:以![]() (单位:万台)表示日销量,
(单位:万台)表示日销量,![]() ,则每位员工每日奖励200元;
,则每位员工每日奖励200元;![]() ,则每位员工每日奖励300元;
,则每位员工每日奖励300元;![]() ,则每位员工每日奖励400元.现已知该公司9月份日销量
,则每位员工每日奖励400元.现已知该公司9月份日销量![]() (万台)服从正态分布
(万台)服从正态分布![]() ,请你计算每位员工当月(按30天计算)获得奖励金额总数大约多少元
,请你计算每位员工当月(按30天计算)获得奖励金额总数大约多少元
参考数据: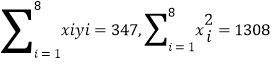 .
.
参考公式:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为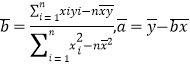
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.