题目内容
13.△ABC的三内角A,B,C的对边分别为a,b,c,已知:a,b,c成等比数列(1)求角B的取值范围;
(2)是否存在实数m,使得不等式(x+3+sin2B)2+[x+$\sqrt{2}$msin(B+$\frac{π}{4}$)]2≥$\frac{1}{8}$对任意的实数x及满足已知条件的所有角B都成立?若存在,求出m的取值范围;若不存在,说明理由.
分析 (1)由已知得b2=ac,由余弦定理及基本不等式可得cosB≥$\frac{1}{2}$,结合范围B∈(0,π),即可解得角B的取值范围.
(2)令t=sinB+cosB=$\sqrt{2}$sin(B+$\frac{π}{4}$),由B∈(0,$\frac{π}{3}$],解得t∈(1,$\sqrt{2}$]且2sinBcosB=t2-1,由题意(x+t2+2)2+(x+mt)2=(x+t2+2)2+(-x-mt)2≥$\frac{(x+{t}^{2}+2-x-mt)^{2}}{2}$=$\frac{({t}^{2}+2-mt)^{2}}{2}$恒成立,仅当x+t2+2=-x-mt,即存在x=$\frac{-{t}^{2}-mt-2}{2}$使“=”成立,即只要$\frac{({t}^{2}+2-mt)^{2}}{2}$$≥\frac{1}{8}$在t∈(1,$\sqrt{2}$]上恒成立,从而可解得m的取值范围.
解答 解:(1)由已知:a,b,c成等比数列,得b2=ac,
在△ABC中,由余弦定理:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$≥$\frac{2ac-{b}^{2}}{2ac}$=$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,当且仅当a=c时,“=”成立,…(3分)
又∵B∈(0,π),∴角B的取值范围为(0,$\frac{π}{3}$]…(5分)
(2)存在满足条件的实数m,取值范围为(-∞,$\sqrt{6}$]∪[$\frac{7}{2}$,+∞).
证明:由题意可得:(x+3+2sinBcosB)2+[x+m(sinB+cosB)]2≥$\frac{1}{8}$对任意的实数x及满足已知条件的所有角B恒成立,
令t=sinB+cosB=$\sqrt{2}$sin(B+$\frac{π}{4}$),
∵B∈(0,$\frac{π}{3}$],∴B+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{7π}{12}$],∴sin(B+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,1],
∴t∈(1,$\sqrt{2}$]且2sinBcosB=t2-1,…(7分)
∴由已知(x+t2+2)2+(x+mt)2$≥\frac{1}{8}$对任意实数x及所有t∈(1,$\sqrt{2}$]上恒成立,
而(x+t2+2)2+(x+mt)2=(x+t2+2)2+(-x-mt)2≥$\frac{(x+{t}^{2}+2-x-mt)^{2}}{2}$=$\frac{({t}^{2}+2-mt)^{2}}{2}$恒成立,
仅当x+t2+2=-x-mt,即存在x=$\frac{-{t}^{2}-mt-2}{2}$使“=”成立,
∴只要$\frac{({t}^{2}+2-mt)^{2}}{2}$$≥\frac{1}{8}$在t∈(1,$\sqrt{2}$]上恒成立 …(9分)
∴2t2-2mt+5≤0或2t2-2mt+3≥0,
即m$≥t+\frac{5}{2t}$或m$≤t+\frac{3}{2t}$,关于t∈(1,$\sqrt{2}$]上恒成立,
令g(t)=t+$\frac{5}{2t}$在t∈(1,$\sqrt{2}$]为减函数,∴g(t)<g(1)=1+$\frac{5}{2}$=$\frac{7}{2}$,
令φ(t)=t+$\frac{3}{2t}$$≥2\sqrt{\frac{3}{2}}=\sqrt{6}$,当且仅当t=$\frac{3}{2t}$,即t=$\sqrt{\frac{3}{2}}∈(1,\sqrt{2}]$时,“=”成立
∴m$≥\frac{7}{2}$或m$≤\sqrt{6}$满足条件,
∴存在满足条件的实数m,取值范围为(-∞,$\sqrt{6}$]∪[$\frac{7}{2}$,+∞).…(12分)
点评 本小题主要考查函数单调性的应用、余弦定理的应用,等比数列的性质的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

| A. | $\frac{1}{7}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{8}$ | D. | $\frac{4}{7}$ |
| A. | 36$\sqrt{3}$+36 | B. | 6$\sqrt{3}$+6 | C. | 3$\sqrt{6}-3\sqrt{2}$ | D. | 18$\sqrt{6}-18\sqrt{2}$ |
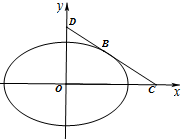 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),离心率e=$\frac{{\sqrt{2}}}{2}$,且过$(\frac{{\sqrt{6}}}{2},\frac{1}{2})$.