题目内容
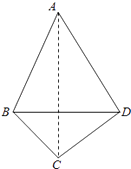
【题目】已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=π/2,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
(1)当x=2时,①求证:BD⊥EG;②求二面角D﹣BF﹣C的余弦值;
(2)三棱锥D﹣FBC的体积是否可能等于几何体ABE﹣FDC体积的一半?并说明理由.
【答案】
(1)①证明:过D点作EF的垂线交EF于H,连接BH.如图.
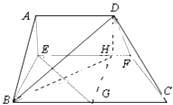
∵AE=AD=2,且AE∥DH,AD∥EF,∠A= ![]() .
.
∴四边形ADHE是正方形
∵EH=2
∴四边形EHGB是正方形
即:BH⊥EG(正方形对角线互为垂直)
∵△BDH所在平面⊥平面EHGB,
∴EG⊥△BDH所在平面
即:BD⊥EG.
②解:以E为原点,EB为x轴,EF为y轴,
EA为z轴,建立空间直角坐标系,
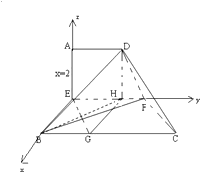
B(2,0,0),F(0,3,0),
D(0,2,2),C(2,4,0),
![]() =(﹣2,3,0),
=(﹣2,3,0), ![]() =(﹣2,2,2),
=(﹣2,2,2),
设平面BDF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 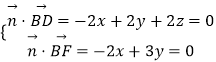 ,取x=3,得
,取x=3,得 ![]() =(3,2,1),
=(3,2,1),
又平面BCF的法向量 ![]() =(0,0,1),
=(0,0,1),
cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
∴二面角D﹣BF﹣C的余弦值为 ![]()
(2)解:∵AE⊥EF,平面AEFD⊥平面EBCF,
平面AEFD∩平面EBCF=EF,AE平面AEFD.
∴AE⊥面EBCF.结合DH⊥平面EBCF,得AE∥DH,
∴四边形AEHD是矩形,得DH=AE,
故以F、B、C、D为顶点的三棱锥D﹣BCF的高DH=AE=x,
又∵S△BCF= ![]() BCBE=
BCBE= ![]() =8﹣2x.
=8﹣2x.
∴三棱锥D﹣BCF的体积为V= ![]() =
= ![]() =
= ![]() ,
,
VABE﹣FDC=VABE﹣DGH+VD﹣HGCF
= ![]()
= ![]()
= ![]() >2V,
>2V,
∴棱锥D﹣FBC的体积不可能等于几何体ABE﹣FDC体积的一半.
【解析】(1)①:过D点作EF的垂线交EF于H,连接BH,由已知得四边形ADHE是正方形,四边形EHGB是正方形,由此能证明BD⊥EG.②以E为原点,EB为x轴,EF为y轴,EA为z轴,建立空间直角坐标系,利用向量法能求出二面角D﹣BF﹣C的余弦值.(2)由已知得三棱锥D﹣BCF的体积为V= ![]() =
= ![]() =
= ![]() ,VABE﹣FDC=VABE﹣DGH+VD﹣HGCF=
,VABE﹣FDC=VABE﹣DGH+VD﹣HGCF= ![]() >2V,从而棱锥D﹣FBC的体积不可能等于几何体ABE﹣FDC体积的一半.
>2V,从而棱锥D﹣FBC的体积不可能等于几何体ABE﹣FDC体积的一半.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中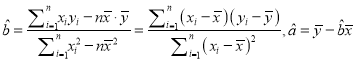 .
.