题目内容
【题目】已知直线l：x+y﹣4=0，定点P（2，0），E，F分别是直线l和y轴上的动点，则△PEF的周长的最小值为（ ）
A.2
B.6
C.3
D.2
【答案】A
【解析】解：如图所示：设P′是点P（2，0）关于直线l：x+y﹣4=0的对称点，设P′（a，b），
则由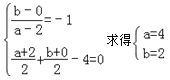
， 可得P′（4，2）．
设P′关于y轴的对称点为P″（m，n），易得P″（﹣4，2），则直线PP″和y轴的交点为F，
FP′和直线l的交点为E，则此时，
△PEF的周长为EF+EP+PF=EF+EP′+PF=P′F+PF=P″F+PF=PP″=2
，
为最小值，
故选：A．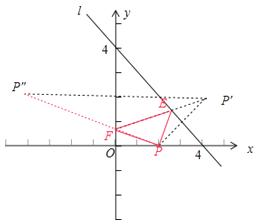
求得点P（2，0）关于直线l：x+y﹣4=0的对称点P′的坐标，再求得P′关于y轴的对称点为P″的坐标，可得此时△PEF的周长的最小值为PP″，计算求得结果．
练习册系列答案
相关题目
