题目内容
5.已知向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$=(1,-2)的夹角为π,|$\overrightarrow{AB}$|=2$\sqrt{5}$,点A的坐标为(3,-4).则点B坐标为( )| A. | (1,0) | B. | (0,1) | C. | (5,-8) | D. | (-8,5) |
分析 由条件利用两个向量的数量积的定义求得$\overrightarrow{a}$•$\overrightarrow{AB}$,设出点B的坐标,再利用两个向量的数量积公式求得$\overrightarrow{a}$•$\overrightarrow{AB}$,可得a、b的一个关系式.再根据向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$=(1,-2)的夹角为π,再得到一个关于a、b的关系式,解方程组求得a、b的值,可得点B坐标.
解答 解:由题意可得|$\overrightarrow{a}$|=$\sqrt{1+4}$=$\sqrt{5}$,∴$\overrightarrow{a}$•$\overrightarrow{AB}$=|$\overrightarrow{a}$|•|$\overrightarrow{AB}$|•cosπ=$\sqrt{5}$•2$\sqrt{5}$•(-1)=-10.
设点B的坐标为(a,b),则$\overrightarrow{AB}$=(a-3,b+4),由 $\overrightarrow{a}$•$\overrightarrow{AB}$=1×(a-3)+(-2)(b+4)=-10,
求得a-2b=1 ①.
再根据向量$\overrightarrow{AB}$与向量$\overrightarrow{a}$=(1,-2)的夹角为π,可得(a-3,b+4)=k(1,-2),k<0,即 b=2-2a ②.
结合①②求得a=1,b=0,故点B的坐标为(1,0),
故选:A.
点评 本题主要考查两个向量的数量积的定义,两个向量的数量积公式,两个向量共线的性质,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.执行如图所示的程序框图,输出的S为( )


| A. | -1006 | B. | 1007 | C. | -1008 | D. | 1009 |
14. 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )| A. | $\frac{10}{3}$ | B. | 3 | C. | $\frac{14}{3}$ | D. | 4 |
 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小. 与
与 的夹角为
的夹角为 ,且
,且 ,若
,若 ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
 的图象上存在两点关于
的图象上存在两点关于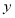 轴对称,则实数
轴对称,则实数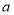 的取值范围是( )
的取值范围是( )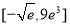 D.
D.
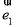 与
与 的夹角为
的夹角为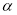 ,且
,且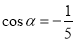 ,若
,若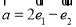 ,
,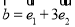 ,则
,则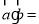 ( )
( )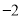 B.
B.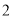
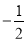 D.
D.
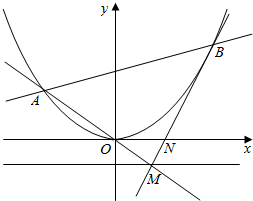 抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.
抛物线C:x2=4y,直线l1:y=kx交C于点A,交准线于点M.过点M的直线l2与抛物线C有唯一的公共点B(A,B在对称轴的两侧),且与x轴交于点N.