题目内容
【题目】已知椭圆![]() 右顶点与右焦点的距离为
右顶点与右焦点的距离为![]() ,短轴长为
,短轴长为![]()
(I)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为![]() 求直线AB的方程。
求直线AB的方程。
【答案】(1)由![]() ;(2)
;(2)![]() 或
或![]()
【解析】(1)由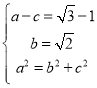 ;(2)利用直线与椭圆的位置关系,研究三角形的面积,利用韦达定理求解直线的方程。
;(2)利用直线与椭圆的位置关系,研究三角形的面积,利用韦达定理求解直线的方程。
解:(Ⅰ)由题意,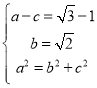 -------1分
-------1分
解得![]() . ------------2分
. ------------2分
即:椭圆方程为![]() ------------4分
------------4分
(Ⅱ)当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,
,
此时![]() 不符合题意故舍掉;
不符合题意故舍掉;
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线 ![]() 的方程为:
的方程为:![]() ,
,
代入消去![]() 得:
得:![]() . ------------5分
. ------------5分
设![]() ,则
,则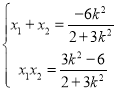 ,
,
所以 ![]() . ------------7分
. ------------7分
原点到直线的![]() 距离
距离![]() ,
,
所以三角形的面积 .
.
由![]() , ------------11分
, ------------11分
所以直线或
![]() . ---------12分
. ---------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目