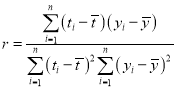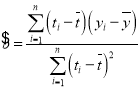题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)记![]() ,当
,当![]() 时,若对任意式
时,若对任意式![]() ,总有
,总有![]() 成立,试求
成立,试求![]() 的最大值.
的最大值.
【答案】(1)![]() 在
在![]() 上是增函数;在
上是增函数;在![]() 上是减函数(2)
上是减函数(2)![]() (3)
(3)![]() 的最大值为
的最大值为![]()
【解析】
(1)求得![]() 的定义域和导函数,由此求得
的定义域和导函数,由此求得![]() 的单调区间.
的单调区间.
(2)求得![]() 的导函数
的导函数![]() ,对
,对![]() 分成
分成![]() ,
,![]() ,
,![]() 三种情况,结合
三种情况,结合![]() 在区间
在区间![]() 上的单调性和最大值,求得
上的单调性和最大值,求得![]() 的值.
的值.
(3)首先求得![]() 的的表达式,利用
的的表达式,利用![]() 的导函数
的导函数![]() 判断出当
判断出当![]() 时,
时,![]() 为减函数,由此将不等式
为减函数,由此将不等式![]() 转化为
转化为![]() ,构造函数
,构造函数![]() ,
,![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 的导函数
的导函数![]() 分离常数
分离常数![]() ,得到
,得到![]() ,结合基本不等式,求得
,结合基本不等式,求得![]() 的最大值.
的最大值.
(1)![]() 的定义域是
的定义域是![]() ,
,![]() ,
,
令![]() ,则
,则![]() (舍去),
(舍去),
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是减函数.
上是减函数.
(2)∵![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
故在![]() 上的最大值为
上的最大值为![]() ,显然不合题意:
,显然不合题意:
②若 即
即![]() 时,
时, ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
故在![]() 上的最大值为
上的最大值为![]() ,不合超意,舍去;
,不合超意,舍去;
③若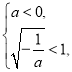 即
即![]() 时,则
时,则![]() 在
在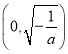 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
故在在![]() 上的最大值为
上的最大值为![]() ,解得
,解得![]() ,符合,
,符合,
综合①②③得![]() .
.
(3)![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,
不妨设![]() ,则
,则![]() ,
,
故![]() 等价于
等价于![]() ,
,
即![]() ,记
,记![]() ,从而
,从而![]() 在
在![]() 上为减函数,
上为减函数,
由![]() ,得
,得![]() ,故
,故![]() 恒成立,
恒成立,
∵![]() ,又
,又![]() 在
在![]() 上单调递减
上单调递减
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
故![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.

【题目】2016年9月15中秋节(农历八月十五)到来之际,某月饼销售企业进行了一项网上调查,得到如下数据:
男 | 女 | 合计 | |
喜欢吃月饼人数(单位:万人) | 50 | 40 | 90 |
不喜欢吃月饼人数(单位:万人) | 30 | 20 | 50 |
合计 | 80 | 60 | 140 |
为了进一步了解中秋节期间月饼的消费量,对参与调查的喜欢吃月饼的网友中秋节期间消费月饼的数量进行了抽样调查,得到如下数据:

已知该月饼厂所在销售范围内有30万人,并且该厂每年的销售份额约占市场总量的35%.
(1)试根据所给数据分析,能否有![]() 以上的把握认为,喜欢吃月饼与性别有关?
以上的把握认为,喜欢吃月饼与性别有关?
参考公式与临界值表: ,
,
其中:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(2)若忽略不喜欢月饼者的消费量,请根据上述数据估计:该月饼厂恰好生产多少吨月饼恰好能满足市场需求?