题目内容
已知极坐标的极点在平面直角坐标系的原点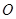 处,极轴与
处,极轴与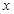 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线 的极坐标方程为:
的极坐标方程为: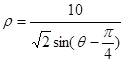 ,点
,点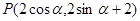 ,参数
,参数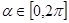 .
.
(Ⅰ)求点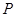 轨迹的直角坐标方程;(Ⅱ)求点
轨迹的直角坐标方程;(Ⅱ)求点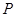 到直线
到直线 距离的最大值.
距离的最大值.
 处,极轴与
处,极轴与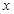 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线 的极坐标方程为:
的极坐标方程为: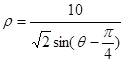 ,点
,点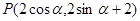 ,参数
,参数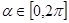 .
.(Ⅰ)求点
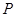 轨迹的直角坐标方程;(Ⅱ)求点
轨迹的直角坐标方程;(Ⅱ)求点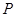 到直线
到直线 距离的最大值.
距离的最大值.(Ⅰ)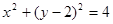 ;(Ⅱ)
;(Ⅱ)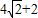
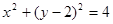 ;(Ⅱ)
;(Ⅱ)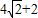
试题分析:(Ⅰ)由
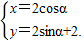 消去θ即求出P轨迹的直角坐标方程;;(Ⅱ)直线l的极坐标方程即为
消去θ即求出P轨迹的直角坐标方程;;(Ⅱ)直线l的极坐标方程即为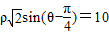 ,化直角坐标方程为x y+10=0,利用直线和圆的位置关系可解.或利用点线距结合三角函数知识求解.
,化直角坐标方程为x y+10=0,利用直线和圆的位置关系可解.或利用点线距结合三角函数知识求解.试题解析:(Ⅰ)由
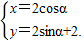 且参数α∈[0,2π],
且参数α∈[0,2π],所以点P的轨迹方程为
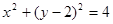 .(3分)
.(3分)(Ⅱ)因为
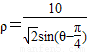 ,所以
,所以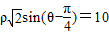 ,
,所以ρsinθ ρcosθ=10,所以直线l的直角坐标方程为x y+10=0.(6分)
法一:由(Ⅰ) 点P的轨迹方程为
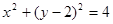 ,圆心为(0,2),半径为2.
,圆心为(0,2),半径为2.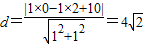 ,所以点P到直线l距离的最大值
,所以点P到直线l距离的最大值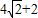 .(10分)
.(10分)法二:
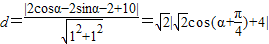 ,当
,当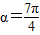 ,
,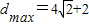 ,即点P到直线l距离的最大值
,即点P到直线l距离的最大值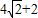 .(10分)
.(10分)
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 轴正半轴.已知曲线
轴正半轴.已知曲线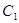 的极坐标方程为
的极坐标方程为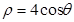 ,曲线
,曲线 的参数方程为
的参数方程为 (其中
(其中 为参数)
为参数)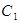 的直角坐标方程和曲线
的直角坐标方程和曲线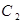 的普通方程;
的普通方程;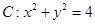 ,直线
,直线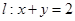 ,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.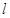 方程化为极坐标方程;
方程化为极坐标方程;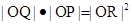 ,当点P在
,当点P在 的参数方程是
的参数方程是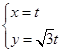 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,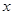 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线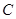 的极坐标方程为
的极坐标方程为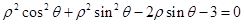 .
.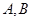 两点,求
两点,求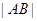 .
. 和
和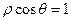 相交于点
相交于点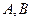 ,则
,则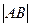 = ;
= ;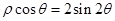 表示的曲线为( )
表示的曲线为( ) 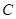 的极坐标方程为
的极坐标方程为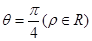 ,直线
,直线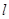 的参数方程为
的参数方程为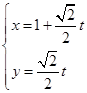 (
(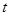 为参数).
为参数).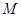 、
、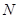 分别是曲线
分别是曲线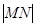 的最小值为 .
的最小值为 . 为极点,以
为极点,以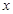 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线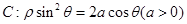 ,过点
,过点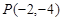 的直线
的直线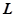 的参数方程为
的参数方程为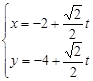 ,设直线
,设直线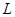 与曲线
与曲线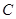 分别交于
分别交于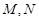 ;
;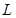 的普通方程;
的普通方程;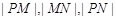 成等比数列,求
成等比数列,求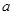 的值.
的值.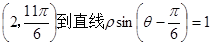 的距离等于____________。
的距离等于____________。