题目内容
给定函数①y=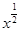 ,②y=
,②y=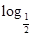 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
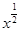 ,②y=
,②y=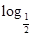 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )| A.①② | B.②③ |
| C.③④ | D.①④ |
B
显然幂函数y=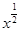 及指数型函数y=2x+1在(0,1)上单调递增,对于y=
及指数型函数y=2x+1在(0,1)上单调递增,对于y=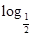 (x+1)可看作是y=
(x+1)可看作是y=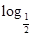 u,
u,
u=x+1的复合函数,由复合函数的单调性知y=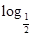 (x+1)在(0,1)上递减,对函数y=|x-1|,其图象是偶函数y=|x|的图象向右平移一个单位得到,y=|x|在(-1,0)上递减,则y=|x-1|在(0,1)上递减.故选B.
(x+1)在(0,1)上递减,对函数y=|x-1|,其图象是偶函数y=|x|的图象向右平移一个单位得到,y=|x|在(-1,0)上递减,则y=|x-1|在(0,1)上递减.故选B.
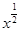 及指数型函数y=2x+1在(0,1)上单调递增,对于y=
及指数型函数y=2x+1在(0,1)上单调递增,对于y=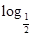 (x+1)可看作是y=
(x+1)可看作是y=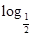 u,
u,u=x+1的复合函数,由复合函数的单调性知y=
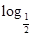 (x+1)在(0,1)上递减,对函数y=|x-1|,其图象是偶函数y=|x|的图象向右平移一个单位得到,y=|x|在(-1,0)上递减,则y=|x-1|在(0,1)上递减.故选B.
(x+1)在(0,1)上递减,对函数y=|x-1|,其图象是偶函数y=|x|的图象向右平移一个单位得到,y=|x|在(-1,0)上递减,则y=|x-1|在(0,1)上递减.故选B.
练习册系列答案
相关题目
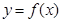 的定义域为
的定义域为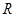 ,若存在常数
,若存在常数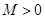 ,使
,使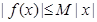 对一切
对一切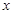 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下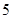 个函数:
个函数: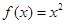 ; ②
; ②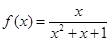 ;③
;③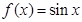 ;④
;④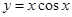 ;
;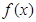 是
是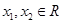 ,均有
,均有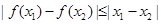 .
.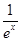 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性. ,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.
,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.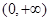 上单调递增的是( )
上单调递增的是( )
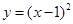
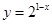
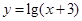
 ),f(-1)的大小关系为( )
),f(-1)的大小关系为( )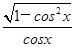 ( ).
( ). 上递增
上递增 上递增,在
上递增,在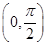 上递减
上递减