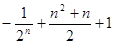题目内容
等比数列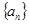 各项为正,
各项为正,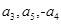 成等差数列.
成等差数列.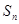 为
为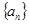 的前n项和,则
的前n项和,则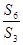 =( )
=( )
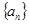 各项为正,
各项为正,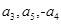 成等差数列.
成等差数列.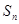 为
为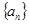 的前n项和,则
的前n项和,则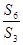 =( )
=( ) | A.2 | B.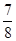 | C.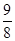 | D.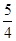 |
C
试题分析:设{an}的公比为q(q≠0,q≠1),利用
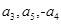 成等差数列结合通项公式,可得
成等差数列结合通项公式,可得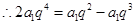 ,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案
,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案设{an}的公比为q(q>0,q≠1)
∵
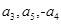 成等差数列,∴
成等差数列,∴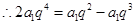
∵a1≠0,q≠0,∴2q2+q-1=0,
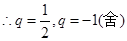 ,故
,故 ,故选C.
,故选C.点评:解决该试题的关键是对于数列公式的熟练表示和运用,属于基础题 。

练习册系列答案
相关题目
 }中,a
}中,a ,前n项和为
,前n项和为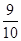 ,则项数n为
,则项数n为 x
x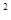 -
-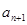 x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.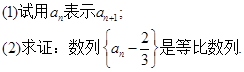
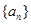 中,
中,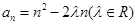 ,若
,若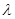 的取值范围为___________.
的取值范围为___________.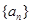 的前
的前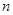 项和为
项和为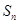 ,且
,且 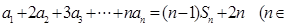 N
N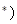 .
. 是三个互不相等的正整数,且
是三个互不相等的正整数,且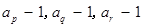 是否成等比数列?并说明理由.
是否成等比数列?并说明理由. 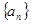 ,满足
,满足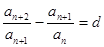
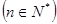 d为常数,我们称
d为常数,我们称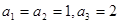 ,则
,则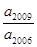 的个位数( )
的个位数( ) 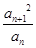 (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)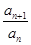 }是不是等比数列?
}是不是等比数列?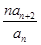 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。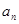 }的公差
}的公差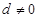 ,它的前n项和为
,它的前n项和为 ,若
,若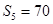 ,且
,且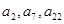 成等比数列,
成等比数列,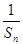 }的前n项和为
}的前n项和为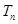 ,求证:
,求证: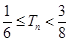 。
。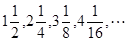 前n项的和为( )
前n项的和为( )