题目内容
【题目】如图,正方体![]() 的棱长为2,P为BC的中点,Q为线段
的棱长为2,P为BC的中点,Q为线段![]() 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是______(写出所有正确命题的编号).
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是______(写出所有正确命题的编号).

①当![]() 时,S为四边形;②当
时,S为四边形;②当![]() 时,S为等腰梯形;③当
时,S为等腰梯形;③当![]() 时,S与
时,S与![]() 的交点R满足
的交点R满足![]() ;④当
;④当![]() 时,S为五边形;⑤当
时,S为五边形;⑤当![]() 时,S的面积为
时,S的面积为![]() .
.
【答案】①②④
【解析】
利用空间几何元素的位置关系和截面的性质逐一分析推理判断每一个命题的真假得解.
对于①,由图1知,
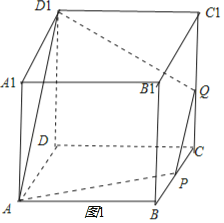
当点Q向C移动时,满足0<CQ<1,只需在DD1上取点M,且满足AM∥PQ,
则截面图形为四边形APQM,∴①正确;
对于②,当CQ=1时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1=![]() ,
,
可得截面APQD1为等腰梯形,∴②正确;
对于③,当CQ=![]() 时,如图2所示,
时,如图2所示,
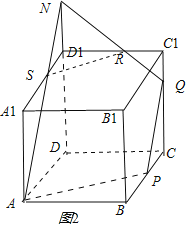
延长DD1至N,使D1N=1,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,可得C1R=![]() ,D1R=
,D1R=![]() ,∴③错误;
,∴③错误;
对于④,当![]() 时,只需点Q上移,此时的截面形状仍然上图所示的APQRS,是五边形,④正确;
时,只需点Q上移,此时的截面形状仍然上图所示的APQRS,是五边形,④正确;
对于⑤,当CQ=2时,Q与C1重合,取A1D1的中点F,连接AF,可证PC1∥AF,且PC1=AF,
可知截面为APC1F为菱形,且面积为![]() AC1PF=2
AC1PF=2![]() ,⑤错误;
,⑤错误;
综上可得:正确命题的序号为①②④.
故答案为:①②④.

练习册系列答案
相关题目




