题目内容
、(12分)设直线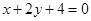 和圆
和圆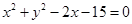 相交于点
相交于点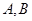 。
。
(1)求弦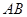 的垂直平分线方程;
的垂直平分线方程;
(2)求弦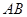 的长。
的长。
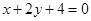 和圆
和圆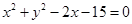 相交于点
相交于点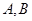 。
。(1)求弦
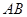 的垂直平分线方程;
的垂直平分线方程;(2)求弦
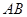 的长。
的长。(1)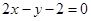 。(2)
。(2) 。
。
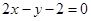 。(2)
。(2) 。
。本试题主要是考查了直线与圆的位置关系的运用,以及两直线的位置关系的综合运用。
(1)先利用直线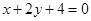 和圆
和圆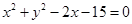 相交于点
相交于点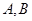 ,易知易知弦
,易知易知弦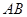 的垂直平分线过圆心,且与直线
的垂直平分线过圆心,且与直线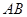 垂直,那么得到直线的斜率和点,从而得到。
垂直,那么得到直线的斜率和点,从而得到。
(2)根据圆心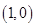 到直线
到直线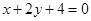 的距离
的距离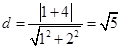 ,结合勾股定理得到弦长的值。
,结合勾股定理得到弦长的值。
解:(1)圆方程可整理为: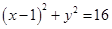 ,
,
所以,圆心坐标为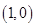 ,半径
,半径 ,
,
易知弦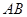 的垂直平分线过圆心,且与直线
的垂直平分线过圆心,且与直线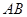 垂直,
垂直,
而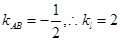 ,
,
所以,由点斜式方程可得: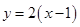 ,
,
整理得: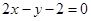 。
。
(2)圆心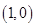 到直线
到直线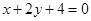 的距离
的距离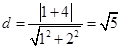 ,
,
故 。
。
(1)先利用直线
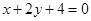 和圆
和圆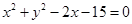 相交于点
相交于点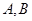 ,易知易知弦
,易知易知弦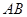 的垂直平分线过圆心,且与直线
的垂直平分线过圆心,且与直线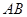 垂直,那么得到直线的斜率和点,从而得到。
垂直,那么得到直线的斜率和点,从而得到。(2)根据圆心
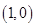 到直线
到直线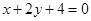 的距离
的距离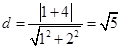 ,结合勾股定理得到弦长的值。
,结合勾股定理得到弦长的值。解:(1)圆方程可整理为:
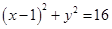 ,
,所以,圆心坐标为
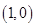 ,半径
,半径 ,
,易知弦
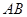 的垂直平分线过圆心,且与直线
的垂直平分线过圆心,且与直线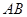 垂直,
垂直,而
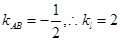 ,
,所以,由点斜式方程可得:
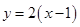 ,
,整理得:
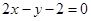 。
。(2)圆心
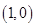 到直线
到直线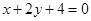 的距离
的距离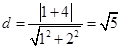 ,
,故
 。
。
练习册系列答案
相关题目
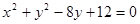 ,直线
,直线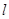 :
: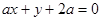 .
.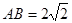 时,求直线
时,求直线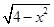 (|x|≤2)与直线y=k(x-2)+4有两个交点时,实数k的取值范围是( )
(|x|≤2)与直线y=k(x-2)+4有两个交点时,实数k的取值范围是( ) 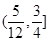
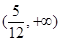
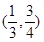

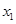 、
、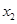 是关于x的方程
是关于x的方程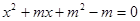 的两个不相等的实数根,那么过两点
的两个不相等的实数根,那么过两点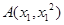 ,
,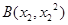 的直线与圆
的直线与圆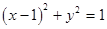 的位置关系是( )
的位置关系是( )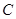 经过
经过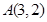 、
、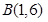 两点,且圆心在直线
两点,且圆心在直线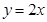 上.
上.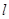 经过点
经过点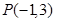 且与圆
且与圆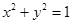 上的点到直线
上的点到直线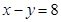 的距离的最小值
的距离的最小值 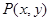 是圆
是圆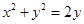 上的动点,
上的动点,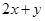 的取值范围;
的取值范围;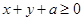 恒成立,求实数
恒成立,求实数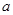 的取值范围。
的取值范围。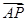 ·
·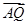 的值为______.
的值为______.