题目内容
已知,圆C: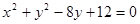 ,直线
,直线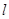 :
: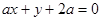 .
.
(1) 当a为何值时,直线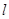 与圆C相切;
与圆C相切;
(2) 当直线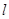 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且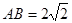 时,求直线
时,求直线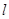 的方程.
的方程.
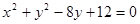 ,直线
,直线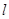 :
: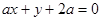 .
.(1) 当a为何值时,直线
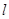 与圆C相切;
与圆C相切;(2) 当直线
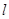 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且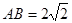 时,求直线
时,求直线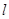 的方程.
的方程. (1) 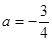 (2) 直线
(2) 直线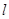 的方程是
的方程是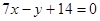 和
和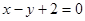
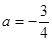 (2) 直线
(2) 直线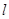 的方程是
的方程是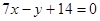 和
和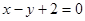
(1)根据圆心到直线的距离等于半径建立关于a的方程,求出a值.
(2)根据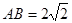 ,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.
,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.
解:将圆C的方程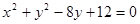 配方得标准方程为
配方得标准方程为 ,则此圆的圆心为(0 , 4),半径为2. ……………………………2分
,则此圆的圆心为(0 , 4),半径为2. ……………………………2分
(1) 若直线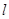 与圆C相切,则有
与圆C相切,则有 . …………………………4分
. …………………………4分
解得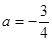 . ……………………6分
. ……………………6分
(2) 解法一:过圆心C作CD⊥AB, ………7分
则根据题意和圆的性质,得
 …………………10分
…………………10分
解得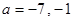 .……………12分
.……………12分
(解法二:联立方程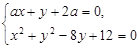 并消去
并消去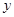 ,得
,得
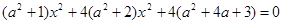 .
.
设此方程的两根分别为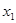 、
、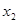 ,则用
,则用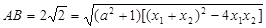 即可求出a.)
即可求出a.)
∴直线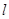 的方程是
的方程是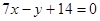 和
和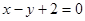 .…………………………14分
.…………………………14分
(2)根据
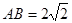 ,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.
,借助弦长公式可求得圆心到直线的距离,从而利用点到直线的距离公式建立关于a的方程,求出a值.解:将圆C的方程
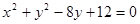 配方得标准方程为
配方得标准方程为 ,则此圆的圆心为(0 , 4),半径为2. ……………………………2分
,则此圆的圆心为(0 , 4),半径为2. ……………………………2分(1) 若直线
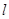 与圆C相切,则有
与圆C相切,则有 . …………………………4分
. …………………………4分解得
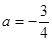 . ……………………6分
. ……………………6分(2) 解法一:过圆心C作CD⊥AB, ………7分
则根据题意和圆的性质,得
 …………………10分
…………………10分解得
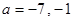 .……………12分
.……………12分(解法二:联立方程
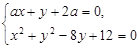 并消去
并消去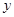 ,得
,得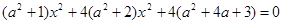 .
.设此方程的两根分别为
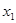 、
、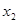 ,则用
,则用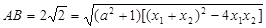 即可求出a.)
即可求出a.)∴直线
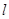 的方程是
的方程是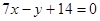 和
和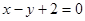 .…………………………14分
.…………………………14分
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
 与圆
与圆 的位置关系是 ( )
的位置关系是 ( ) 满足
满足 ,那么
,那么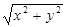 的最小值为
的最小值为  的极坐标方程为
的极坐标方程为 ,则圆
,则圆
 的最短距离为 .
的最短距离为 .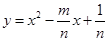 的图象在点
的图象在点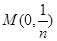 处的切线
处的切线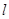 与圆
与圆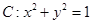 相交,则点
相交,则点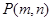 与圆
与圆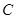 的位置关系是( )
的位置关系是( )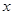 轴的正半轴上,且与直线
轴的正半轴上,且与直线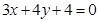 相切,则
相切,则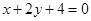 和圆
和圆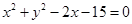 相交于点
相交于点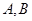 。
。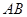 的垂直平分线方程;
的垂直平分线方程;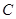 :
: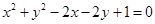 ,
,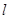 :
: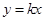 ,且
,且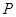 、
、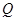 两点,点
两点,点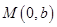 ,且
,且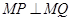 .
.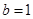 时,求
时,求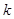 的值;
的值;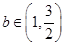 ,求
,求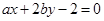
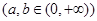 平分圆
平分圆 ,则
,则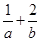 的最小值是
的最小值是