题目内容
【题目】已知下列各命题：
①两两相交且不共点的三条直线确定一个平面：
②若真线
不平行于平面，则直线与平面有公共点：
③若两个平面垂直，则一个平面内的已知直线必垂直于另一个平面的无数条直线：
④若两个二面角的两个面分别对应垂直，则这两个二面角相等或互补.
则其中正确的命题共有（ ）个
A.
B.
C.
D.
【答案】B
【解析】
①利用平面的基本性质判断.②利用直线与平面的位置关系判断.③由面面垂直的性质定理判断.④通过举反例来判断.
①两两相交且不共点，形成三个不共线的点，确定一个平面，故正确.
②若真线
不平行于平面，则直线与平面相交或在平面内，所以有公共点，故正确.
③若两个平面垂直，则一个平面内，若垂直交线的直线则垂直另一个平面，垂直另一平面内所有直线，若不垂直与交线，也与另一平面内垂直交线的直线及其平行线垂直，也有无数条，故正确.
④若两个二面角的两个面分别对应垂直，则这两个二面角关系不确定，如图：
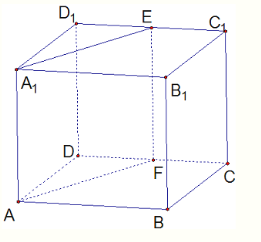
在正方体ABCD-A1B1C1D1中，二面角D-AA1-F与二面角D1-DC-A的两个半平面就是分别对应垂直的，但是这两个二面角既不相等，也不互补．故错误..
故选：B
练习册系列答案
同步练习强化拓展系列答案
相关题目
