题目内容
18.函数f(x)上任意一点A(x1,y1)处的切线l1,在其图象上总存在异于点A的点B(x2,y2),使得在点B处的切线l2满足l1∥l2,则称函数具有“自平行性”,下列有关函数f(x)的命题:①函数f(x)=sinx+1具有“自平行性”;
②函数f(x)=x3(-1≤x≤2)具有“自平行性”;
③函数f(x)=$\left\{\begin{array}{l}{{e}^{x}-1(x<0)}\\{x+\frac{1}{x}(x>m)}\end{array}\right.$具有“自平行性”的充要条件为函数m=1;
④奇函数y=f(x)(x≠0)不一定具有“自平行性”;
⑤偶函数y=f(x)具有“自平行性”.
其中所有叙述正确的命题的序号是①③④.
分析 根据已知中函数具有“自平行性”的定义,逐一分析5个函数是否具有“自平行性”,最后综合讨论结果,可得答案.
解答 解:函数f(x)具有“自平行性”,即对定义域内的任意自变量x1,总存在x2≠x1,使得f′(x1)=f′(x2).
对于①,f′(x)=cosx,具有周期性,必满足条件,故①正确;
对于②,f′(x)=3x2(-1≤x≤2),对任意x1∈(1,2],不存在x2≠x1,使得f′(x1)=f′(x2)成立,故②错误;
对于③,当x<0时,f′(x)=ex∈(0,1),而x>m时,f′(x)=1-$\frac{1}{{x}^{2}}$∈(0,1),解得x<-1(舍去),或x>1,则m=1,故③正确;
对于④,f(x)=x,(x≠0)不符合定义,故④正确;
对于⑤,同④,其导函数为奇函数,故⑤不正确.
故答案为:①③④.
点评 本题以命题的真假判断为载体,考查了函数具有“自平行性”的定义,正确理解函数具有“自平行性”的定义,是解答的关键.

练习册系列答案
相关题目
8.若x<0,则x+$\frac{1}{x}$的最大值是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
6.某中学一名数学老师对全班50名学生某次考试成绩分男女进行了统计(满分150分),得到右面频率分布表:其中120分(含120分)以上为优秀.
(1)根据以上频率表的数据,完成下面的2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间的关系?
(3)若从成绩及在[130,140]的学生中任取3人,已知取到的第一个人是男生,求取到的另外2人中至少有1名女生的概率.
(1)根据以上频率表的数据,完成下面的2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间的关系?
(3)若从成绩及在[130,140]的学生中任取3人,已知取到的第一个人是男生,求取到的另外2人中至少有1名女生的概率.
| 分组 | 频率 | |
| 男生 | 女生 | |
| [80,90] | 0 | 0.02 |
| [90,100] | 0.04 | 0.08 |
| [100,110] | 0.06 | 0.12 |
| [110,120] | 0.10 | 0.18 |
| [120,130] | 0.18 | 0.10 |
| [130,140] | 0.08 | 0.04 |
3.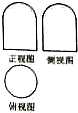 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
 已知函数f(x)=loga(2x+b-l)(a>0,a≠1的图象如图所示,则函数g(x)=ax-b的图象为( )
已知函数f(x)=loga(2x+b-l)(a>0,a≠1的图象如图所示,则函数g(x)=ax-b的图象为( )


