题目内容
10．已知方程$\sqrt{1-（x-2）^{2}}$=x+m有两个不相等的实数根，则实数m的范围是[-1，$\sqrt{2}$-2）．分析 作y=$\sqrt{1-（x-2）^{2}}$与y=x+m的图象，利用数形结合求解即可．
解答 解：作y=$\sqrt{1-（x-2）^{2}}$与y=x+m的图象如下，
结合图象可知，
当m=$\sqrt{2}$-2时，直线与半圆相切，
当m=-1时，直线与半圆有两个交点；
故实数m的取值范围为[-1，$\sqrt{2}$-2）；
故答案为：[-1，$\sqrt{2}$-2）．
点评 本题考查了函数的几何意义的应用及数形结合的思想应用．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
如图所示，已知正方形ABCD所在平面垂直于矩形ACEF所在平面，AB=2，AF=1，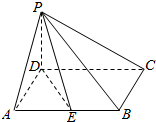
已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，点E为AB中点．
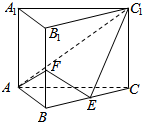已知在直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=2，E，F分别是BC，BB1的中点．