题目内容

10．半径为5的球面上有A、B、C、D四点，若AB=6，CD=8，则四面体ABCD的体积的最大值是56．

分析 四面体ABCD的体积的最大值，AB与CD是对棱，必须垂直，确定球心的位置，即可求出体积的最大值

解答 解：过CD作平面PCD，使AB⊥平面PCD，交AB与P，设点P到CD的距离为h，
则有四面体ABCD的体积=$\frac{1}{3}$×$\frac{1}{2}×8h×6$=8h，
当某条直径通过AB与CD的中点时，hmax=$\sqrt{25-9}$+$\sqrt{25-16}$=7
故Vmax=56．
故答案为：56．

点评 本小题主要考查几何体的体积的计算、球的性质、异面直线的距离，通过球这个载体考查考生的空间想象能力及推理运算能力．

练习册系列答案
相关题目
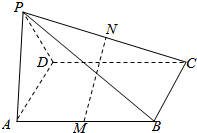11．如图，四棱锥P-ABCD的底面ABCD是平行四边形，M、N分别是AB、PC的中点，且MN⊥PC，MN⊥AB．证明：平面PAD⊥平面PDC．
1．在长方体ABCD-A′B′C′D′中，AB=BC=2，过A′，C′，B三点的平面截去长方体的一个角后，得到ABCD-A′C′D′，
（Ⅰ）若DD′=3，求几何体ABCD-A′C′D′的体积；
（Ⅱ）若DD′＞1，且直线A′D与平面A′BC′所成的角的正弦值为$\frac{4\sqrt{5}}{15}$，求二面角D-A′B-C′的平面角的余弦值．
18．如图，在边长为4的菱形ABCD中，∠DAB=60°，点E、F分别是边CD、CB的中点，AC交EF于点O，沿EF将△CEF翻折到△PEF，连接PA、PB、PD，得到五棱锥P-ABFED，且PB=$\sqrt{10}$．

（1）求证：BD⊥平面POA；
（2）求四棱锥P-BDEF的体积；
（3）求二面角B-AP-O的正切值．
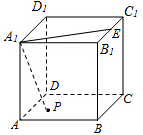5．如图，正方体ABCD-A1B1C1D1中，E是棱B1C1的中点，动点P为正方体各面上的任一点．
①若动点P是AD的中点，则A1E∥平面C1CP；
②若动点P在底面ABCD内，且PA1=A1E，则点P运动轨迹为一条线段；
③若动点P是CC1的中点，则A1E，DP为异面直线；
④若动点P与C点重合，则平面A1EP截该正方体所得的截面的形状为菱形．
以上为真命题的序号的是（　　）
A．①②B．①④C．②④D．③④
15．已知a，b为异面直线，求证：过a和b平行的平面α有且只有一个．
2．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的实轴长为4$\sqrt{2}$，虚轴的一个端点与抛物线x2=2py（p＞0）的焦点重合，直线y=kx-1与抛物线相切且与双曲线的一条渐近线平行，则p=4．
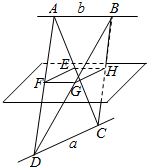19．如图，平面EFGH分别平行于CD，AB，点E，F，G，H分别在AC，AD，BD，BC上，且CD=a，AB=b，CD⊥AB．
（1）求证：四边形EFGH是矩形；
（2）点E在什么位置时，四边形EFGH的面积最大？
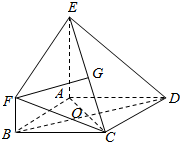20．在如图所示的几何体中，底面ABCD是边长为2的菱形，∠ABC=60°，EA⊥平面ABCD，EA∥BF，EA=2BF=2，G为CE的中点，直线AC与BD相交于点O
（1）求证：FG⊥平面EAC；
（2）求二面角B-DE-C的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网