题目内容
19.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为2,焦点到渐近线的距离为2$\sqrt{3}$.分析 求出双曲线的a,b,c,由离心率公式可得;求得焦点和渐近线方程,由点到直线的距离公式,可得所求距离.
解答 解:双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的a=2,b=2$\sqrt{3}$,c=4,
即有e=$\frac{c}{a}$=2;
焦点为(±4,0),渐近线方程为y=±$\sqrt{3}$x,
即有焦点到渐近线的距离为d=$\frac{|4\sqrt{3}|}{\sqrt{1+3}}$=2$\sqrt{3}$.
故答案为:2,2$\sqrt{3}$.
点评 本题考查双曲线的方程和性质,主要考查离心率的求法和渐近线方程的运用,考查点到直线的距离公式的运用,属于基础题.

练习册系列答案
相关题目
11.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(89)+f(90)为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
9.若f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,则f(2x)等于( )
| A. | 2f(x) | B. | 2[f(x)+g(x)] | C. | 2g(x) | D. | 2f(x)•g(x) |
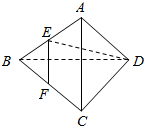 如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.
如图,在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,则正三棱锥A-BCD的体积是$\frac{\sqrt{2}}{3}$.