题目内容
7.如图在三棱锥S-ABC中,SC⊥面ABC,AC⊥BC,且SC=AC=BC,求二面角S-AB-C的余弦值.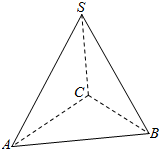
分析 取AB中点O,连结SO,CO,由已知得∠SOC是二面角S-AB-C的平面角,由此能求出二面角S-AB-C的余弦值.
解答  解:设SC=AC=BC=a,
解:设SC=AC=BC=a,
取AB中点O,连结SO,CO,
∵在三棱锥S-ABC中,SC⊥面ABC,AC⊥BC,且SC=AC=BC,
∴SA=SB=AB=$\sqrt{2}a$,
∴SO⊥AB,CO⊥AB,
∴∠SOC是二面角S-AB-C的平面角,
∵CO=AO=$\frac{1}{2}AB$=$\frac{\sqrt{2}}{2}a$,∴SO=$\sqrt{(\frac{\sqrt{2}}{2}a)^{2}+{a}^{2}}$=$\frac{\sqrt{6}}{2}a$,
∴cos∠SOC=$\frac{CO}{SO}$=$\frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{6}}{2}a}$=$\frac{\sqrt{3}}{3}$.
即二面角S-AB-C的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
12. 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
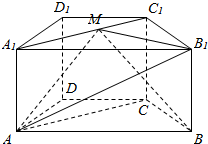 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1. 在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED.
在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴是短轴的两倍,点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为k1、k、k2,且k1、k、k2恰好构成等比数列.