题目内容
15.用五点法画函数f(x)=2sin2x在长度为一个周期的闭区间上的简图.| x | |||||
| 2x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x)=2sin2x |
分析 根据“五点法”即可画出函数在长度为一个周期的闭区间上的简图.
解答 解:①列表:
| x | 0 | $\frac{π}{4}$ | $\frac{π}{2}$ | $\frac{3π}{4}$ | π |
| 2x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| f(x)=2sin2x | 0 | 2 | 0 | -2 | 0 |
③用光滑的曲线连接这五点,得所要求作的函数图象如下:
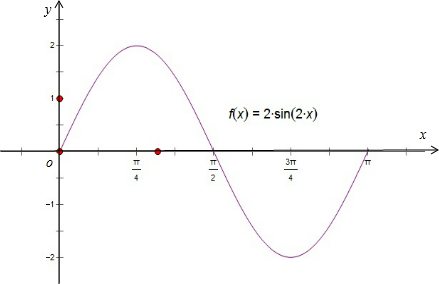
点评 本题主要考查三角函数的图象和性质,要求熟练掌握五点法作图以及函数图象之间的变化关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
3.已知数列{an}的前n项和为Sn,且Sn=n2+1,则下列结论正确的是( )
| A. | an=2n-1 | B. | an=2n+1 | C. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n-1(n>1)}\end{array}}\right.$ | D. | an=$\left\{{\begin{array}{l}{2(n=1)}\\{2n+1(n>1)}\end{array}}\right.$ |
7.已知函数f(x)是定义在R上的奇函数,f(1)=0,当x>0时,有$\frac{xf'(x)-f(x)}{x^2}>0$成立,则不等式x•f(x)>0的解集是( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (1,+∞) | D. | (-1,0)∪(1,+∞) |
5.若O为△ABC所在平面内一点,且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+7$\overrightarrow{OC}$=$\overrightarrow{0}$,则△OAB和△ABC的面积之比为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |